
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
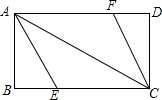 同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
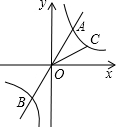 如图.过原点O的直线y=k1x和y=k2x与反比例$\frac{1}{x}$(x>0)的象分别交于点A、C.
如图.过原点O的直线y=k1x和y=k2x与反比例$\frac{1}{x}$(x>0)的象分别交于点A、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩 | 划记 | 频数 |
| 不及格 | 正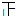 | 9 |
| 及格 | 正正正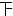 | 18 |
| 良好 | 正正正正正正一 | 36 |
| 优秀 | 正正正正正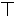 | 27 |
| 合计 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
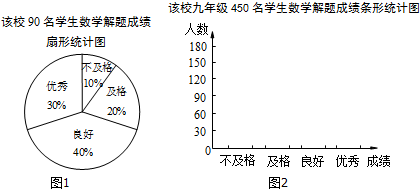
 如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com