
 某班数字兴趣小组利用数学活动课时间测量一座山顶的雕像高度,已知山坡面BD与水平面DC的夹角为30°,山高BC为285.5米,组员从山脚D处沿山坡向着雕像方向前进540米到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度.
某班数字兴趣小组利用数学活动课时间测量一座山顶的雕像高度,已知山坡面BD与水平面DC的夹角为30°,山高BC为285.5米,组员从山脚D处沿山坡向着雕像方向前进540米到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度. 分析 作EF⊥AC于F,EG⊥DC于G,根据直角三角形的性质求出EG,根据题意出去BF,根据正切的定义求出AF,计算即可.
解答 解:作EF⊥AC于F,EG⊥DC于G,
在Rt△DEG中,EG=$\frac{1}{2}$DE=270,
∴BF=BC-CF=285.5-270=15.5,
EF=$\frac{BF}{tan∠BEF}$=$\frac{31}{2}$$\sqrt{3}$,
∵∠AEF=60°,
∴∠A=30°,
∴AF=$\frac{EF}{tanA}$=46.5,
∴AB=AF-BF=15.5(米),
答:雕像AB的高度为15.5米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )
如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )| A. | 4π | B. | 8π | C. | 10π | D. | 15π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
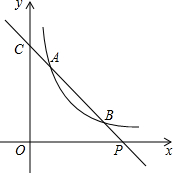 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.已知A,B两点的坐标分别为(1,3),(3,y2).
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.已知A,B两点的坐标分别为(1,3),(3,y2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com