
【题目】如图,已知在矩形ABCD中,BC=2CD=2a,点E在边CD上,在矩形ABCD的左侧作矩形ECGF,使CG=2GF=2b,连接BD,CF,连结AF交BD于点H.

(1)求证:BD∥CF;
(2)求证:H是AF的中点;
(3)连结CH,若HC⊥BD,求a:b的值.
【答案】(1)见解析;(2)见解析;(3)a:b=![]() .
.
【解析】
试题分析:(1)由矩形的性质可知∠G=∠DCB=90°,由BC=2CD=2a,CG=2GF=2b,可知![]() ,依据两边对应成比例且夹角相等的两个三角形相似可知:△FGC∽△DCB,由相似三角形的性质可知∠FCG=∠DBC,由平行线的判定定理可知:BD∥CF;
,依据两边对应成比例且夹角相等的两个三角形相似可知:△FGC∽△DCB,由相似三角形的性质可知∠FCG=∠DBC,由平行线的判定定理可知:BD∥CF;
(2)如图1所示:连接AC,交BD于点O.由矩形的性质可知:OC=OA,由平行线分线段成比例定理可知HF=AH;
(3)如图2所示:连接CH,CA,AC与BD交于点O.由勾股定理可知:FC=![]() b,AC=
b,AC=![]() a,由矩形的对角线的性质可知DB=AC=
a,由矩形的对角线的性质可知DB=AC=![]() a,CO=
a,CO=![]() AC=
AC=![]() .由(2)可知HO是△AFC的中位线,由三角形中位线的性质可知:HO=
.由(2)可知HO是△AFC的中位线,由三角形中位线的性质可知:HO=![]() .在△BCD中,利用面积法可求得CH=
.在△BCD中,利用面积法可求得CH=![]() ,最后在△COH中,由勾股定理得到:(
,最后在△COH中,由勾股定理得到:(![]() )2+(
)2+(![]() )2=(
)2=(![]() a)2,从而可求得a:b=
a)2,从而可求得a:b=![]() .
.
解:(1)∵四边形ABCD、四边形ECGF均为矩形,
∴∠G=∠DCB=90°.
∵BC=2CD=2a,CG=2GF=2b,
∴![]() .
.
∴△FGC∽△DCB.
∴∠FCG=∠DBC.
∴BD∥CF.
(2)如图1所示:连接AC,交BD于点O.
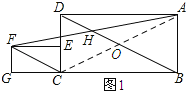
∵四边形ABCD为矩形,
∴OC=OA.
又∵FC∥BD,
∴HF=AH.
∴点H是AF的中点.
(3)如图2所示:连接CH,CA,AC与BD交于点O.
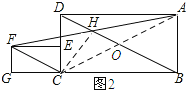
由勾股定理可知:FC=![]() =
=![]() b,AC=
b,AC=![]() =
=![]() a.
a.
∵四边形ABCD为矩形,
∴DB=AC=![]() a,CO=
a,CO=![]() AC=
AC=![]() .
.
∵HO是△AFC的中位线,
∴HO=![]() FC=
FC=![]() .
.
∵![]() ,
,
∴CH=![]() =
=![]() .
.
在△COH中,由勾股定理可知:HO2+CH2=OC2,即(![]() )2+(
)2+(![]() )2=(
)2=(![]() a)2.
a)2.
整理得:a2=![]() .
.
∴a:b=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(﹣2,3)向右平移3个单位长度后的坐标为( )
A. (3,6) B. (1,3) C. (1,6) D. (6,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】笔记本每本a元,买3本笔记本共支出y元,在这个问题中:
①a是常量时,y是变量;
②a是变量时,y是常量;
③a是变量时,y也是变量;
④a,y可以都是常量或都是变量;
上述判断正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
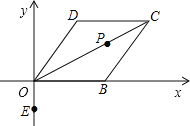
(1)点D的坐标为 ,点C的坐标为 ;
(2)若点P是对角线OC上一动点,点E(0,﹣![]() ),求PE+PB的最小值.
),求PE+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
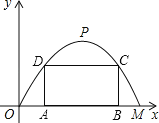
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD﹣DC﹣CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com