
【题目】如图,已知直线l及其两侧两点A、B.

(1)在直线l上求一点O,使到A、B两点距离之和最短;
(2)在直线l上求一点P,使PA=PB;
(3)在直线l上求一点Q,使l平分∠AQB.
【答案】见解析
【解析】
试题分析:(1)根据两点之间线段最短,连接AB,线段AB交直线l于点O,则O为所求点;
(2)根据线段垂直平分线的性质连接AB,在作出线段AB的垂直平分线即可;
(3)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,由三角形全等的判定定理求出△BDQ≌△B′DQ,再由全等三角形的性质可得出∠BQD=∠B′QD,即直线l平分∠AQB.
解:(1)连接AB,线段AB交直线l于点O,
∵点A、O、B在一条直线上,
∴O点即为所求点;

(2)连接AB,
分别以A、B两点为圆心,以任意长为半径作圆,两圆相交于C、D两点,连接CD与直线l相交于P点,
连接BD、AD、BP、AP、BC、AC,
∵BD=AD=BC=AC,
∴△BCD≌△ACD,
∴∠BED=∠AED=90°,
∴CD是线段AB的垂直平分线,
∵P是CD上的点,
∴PA=PB;
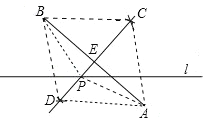
(3)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,
∵B与B′两点关于直线l对称,
∴BD=B′D,DQ=DQ,∠BDQ=∠B′DQ,
∴△BDQ≌△B′DQ,
∴∠BQD=∠B′QD,即直线l平分∠AQB.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B1线路的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,那么抽中20元奖品的概率为
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组线段能构成直角三角形的一组是( )
A. 5 cm, 9 cm,12 cm B. 7 cm,12 cm,13 cm
C. 30 cm,40 cm,50 cm D. 3 cm,4 cm, 6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
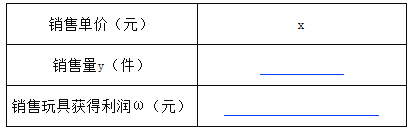
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
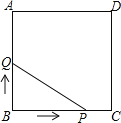
A.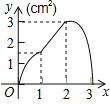 B.
B.
C.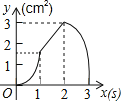 D.
D.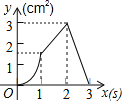
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.矩形的对角线互相垂直
C.一组对边平行的四边形是平行四边形
D.四边相等的四边形是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com