Question

【题目】在四边形ABCD中,∠A=140°,∠D=80°.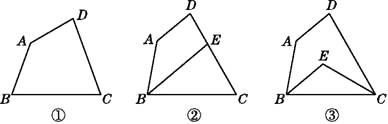

（1）如图①,若∠B=∠C,试求出∠C的度数;
（2）如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
（3）如图③,若∠ABC和∠BCD的平分线交于点E,试求出∠BEC的度数.

Answer 1

【答案】
（1）解:∵∠A+∠B+∠C+∠D=360°,∠B=∠C,∴∠B=∠C=(360°-∠A-∠D)÷2=70°
（2）解:∵BE∥AD,∴∠BEC=∠D=80°,∠ABE+∠A=180°.
∴∠ABE=180°-∠A=180°-140°=40°.
又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60° （2）
（3）解:∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°.
∵∠ABC和∠BCD的平分线交于点E,
∴∠EBC= ∠ABC,∠BCE= ∠BCD.
∴∠EBC+∠BCE=（∠ABC+∠BCD）=×140°=70°，
∴∠E=180°-（∠EBC+∠BCE）=180°-70°=110°
【解析】（1）根据四边形的内角和为360°结合已知∠B=∠C，就可求出∠C的度数。
（2）根据平行线的性质得出∠BEC=∠D=80°,∠ABE+∠A=180°，就可求出∠ABE的度数，再根据角平分线的定义就可求出∠EBC的度数，然后根据三角形的内角和定理就可求出∠C的度数。
（3）根据四边形ABCD中已知∠A和∠D的度数，就可求出∠ABC+∠BCD的度数，再根据角平分线定义求出∠EBC和∠BCE的和，然后根据三角形的内角和定理就可求出∠BEC的度数。