
分析 根据关于原点对称的点的坐标特点找出A、B两点坐标的关系,再根据反比例函数图象上点的坐标特点解答即可.
解答 解:∵函数y=$\frac{\sqrt{2}}{x}$与y=2x图象交于点A(x1,y1)、B(x2,y2),
∴这两点关于原点对称,
即x1=-x2,y1=-y2,
∵A、B都在y=$\frac{\sqrt{2}}{x}$上,
∴x1y1=$\sqrt{2}$,x2y2=$\sqrt{2}$,
∴x1y2+x2y1
=-x1y1-x1y1
=-2x1y1
=-2×$\sqrt{2}$
=-2$\sqrt{2}$.
故答案为:-2$\sqrt{2}$.
点评 本题考查了反比例函数图象的对称性,难度一般,解答本题的关键是利用过原点的直线与双曲线的两个交点关于原点对称.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
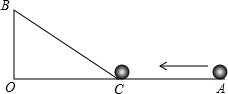 如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com