
分析 (1)求得二次函数的对称轴为y=-$\frac{b}{2a}$=-$\frac{t}{2}$,然后分①-$\frac{t}{2}$≤-1,②-1<-$\frac{t}{2}$<1,③-$\frac{t}{2}$≥1三种情况,根据二次函数的增减性解答.
(3)求得二次函数的对称轴为y=-$\frac{b}{2a}$=-$\frac{t}{2}$,然后分①-$\frac{t}{2}$≤-1,②-1<-$\frac{t}{2}$<0,③-$\frac{t}{2}$=0,④0<-$\frac{t}{2}$<1,⑤-$\frac{t}{2}$≥1五种情况,根据二次函数的增减性解答.
解答 解:(1)∵y=x2+tx+1对称轴为y=-$\frac{b}{2a}$=-$\frac{t}{2}$,且a=1>0,
①-$\frac{t}{2}$≤-1时,-1≤x≤1范围内,y随x的增大而增大,
当x=-1时,y最小,最小值y=1-t+1=2-t,
②-1<-$\frac{t}{2}$<1时,
当x=-$\frac{t}{2}$时有最小值,最小值y=(-$\frac{t}{2}$)2-$\frac{t}{2}$×t+1=1-$\frac{{t}^{2}}{4}$,
③-$\frac{t}{2}$≥1时,-1≤x≤1范围内,y随x的增大而减小,
当x=1时,y最小,最小值y=1+t+1=2+t;
(2)∵y=x2+tx+1对称轴为y=-$\frac{b}{2a}$=-$\frac{t}{2}$,且a=1>0,
①-$\frac{t}{2}$≤-1时,-1≤x≤1范围内,y随x的增大而增大,
当x=1时,y最大,最大值y=1+t+1=2+t;
②-1<-$\frac{t}{2}$<0时,当x=-1有最大值,最大值y=1-t+1=2-t,
③-$\frac{t}{2}$=0时,x=1或-1时有最大值,最大值y=1+1=2,
④0<-$\frac{t}{2}$<1时,当x=1有最大值,最大值y=1+t+1=2+t;
⑤-$\frac{t}{2}$≥1时,-1≤x≤1范围内,y随x的增大而减小,
当x=-1时,y最大,最大值y=1-t+1=2-t.
点评 本题考查了二次函数的最值问题,主要利用了二次函数的增减性,注意根据二次函数的对称轴分情况讨论求解.


科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{9}{8}$ | B. | m≥$\frac{9}{8}$ | C. | m≤$\frac{9}{8}$ | D. | m<$\frac{9}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
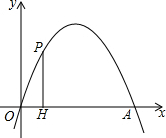 如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.
如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(单位:岁) | 17 | 20 | 23 | 27 | 30 | 33 |
| 人 数 | 1 | 2 | 2 | 4 | 2 | 1 |
| A. | 27,23 | B. | 27,27 | C. | 27,25 | D. | 27,28.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
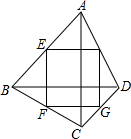 几何证明.
几何证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com