
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统汁图,请根据图中信息解答下列问题:
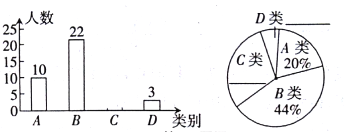
(l)本次抽取样本容量为____,扇形统计图中A类所对的圆心角是____度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
【答案】(1)50,72;(2)详见解析;(3)90名.
【解析】试题分析:(1)用A类学生的人数除以A类学生的人数所占的百分比即可得到抽查的学生数,从而可以求得样本容量,由扇形统计图可以求得扇形圆心角的度数;(2)根据统计图可以求得C类学生数和C类与D类所占的百分比,从而可以将统计图补充完整;(3)用该校九年级男生的人数乘以该校九年级男生“引体向上”项目成绩为C类的的学生所占得百分比即可得答案.
试题解析:(1)由题意可得,
抽取的学生数为:10÷20%=50,
扇形统计图中A类所对的圆心角是:360°×20%=72°,
(2)C类学生数为:50﹣10﹣22﹣3=15,
C类占抽取样本的百分比为:15÷50×100%=30%,
D类占抽取样本的百分比为:3÷50×100%=6%,
补全的统计图如所示,

(3)300×30%=90(名)
即该校九年级男生“引体向上”项目成绩为C类的有90名.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,AC=DF;
④∠A=∠D,∠B=∠E,∠C=∠F.
其中,能使△ABC≌△DEF的条件共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.

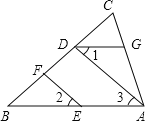
图⑴ 图⑵
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com