
����Ŀ����ͼ��գ���ע�����ɣ�
�������ȷ��֤������ͼ����֪AB��CD����֤����BED=��B+��D
֤������E����EF��AB������ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�У�
���1= �� ��
��AB��CD����֪��
��EF��CD���������ֱ����ͬһֱ��ƽ�У���ô����Ҳƽ�У�
���2= �� ��
�֡�BED=��1+��2
���BED=��B+��D ��������������
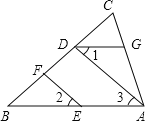
����ͼ���ڡ�ABC�У�EF��AD����1=��2����BAC=70�㣮�����AGD�Ĺ�����д������
�⣺��ΪEF��AD����֪��
���ԡ�2=��3���� ��
����Ϊ��1=��2�����ԡ�1=��3��������������
����AB�� �� ��
���ԡ�BAC+ =180�㣨 ����
����Ϊ��BAC=70�㣬���ԡ�AGD=110�㣮

ͼ�� ͼ��
���𰸡�(1) ��B ����ֱ��ƽ�У��ڴ�����ȣ�
��D ����ֱ��ƽ�У��ڴ�����ȣ�
(2) ����ֱ��ƽ�У�ͬλ����ȣ���
DG ���ڴ�����ȣ���ֱ��ƽ�У���
��AGD ����ֱ��ƽ�У�ͬ���ڽǻ�����
����������������1������ƽ���ߵ����ʽ�����⣻��2������ƽ���ߵ��ж���������⣮
���������
֤������E����EF��AB������ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�У�
���1= ��B ����ֱ��ƽ�У��ڴ�����ȣ�
��AB��CD����֪��
��EF��CD���������ֱ����ͬһֱ��ƽ�У���ô����Ҳƽ�У�
���2= ��D ����ֱ��ƽ�У��ڴ�����ȣ�
�֡�BED=��1+��2
���BED=��B+��D ��������������
����ͼ���ڡ�ABC�У�EF��AD����1=��2����BAC=70�㣮�����AGD�Ĺ�����д������
�⣺��ΪEF��AD����֪��
���ԡ�2=��3������ֱ��ƽ�У�ͬλ����ȣ�
����Ϊ��1=��2�����ԡ�1=��3��������������
����AB�� DG ���ڴ�����ȣ���ֱ��ƽ�У�
���ԡ�BAC+ ��AGD =180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�������
����Ϊ��BAC=70�㣬���ԡ�AGD=110�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
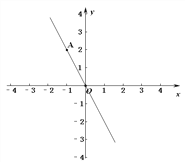
����Ŀ��һ�κ���y1=kx+3������������y2=-2x���ڵ�A��-1��2��.
(1)ȷ��һ�κ�������ʽ��
(2)��xȡ��ֵʱ��y1<0?
(3)��xȡ��ֵʱ��y1>y2?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽ⱾУ���꼶�������������ϡ���Ŀ��ѵ������������ȡ���꼶��������������һ�β��ԣ�����15�֣��ɼ�����Ϊ�����֣����������Գɼ�����λ���֣��ֳ����ࣺA��(12��m��15)��B��(9��m��11),C��(6��m��8),D��(m��5)���Ƴ�����������������ͳ֭ͼ�������ͼ����Ϣ����������⣺
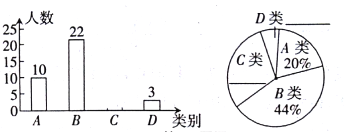
(l)���γ�ȡ��������Ϊ____������ͳ��ͼ��A�����Ե�Բ�Ľ���____�ȣ�
(2)�벹ȫͳ��ͼ��
(3)����У���꼶������300��������Ƹ�У���꼶�������������ϡ���Ŀ�ɼ�ΪC����ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
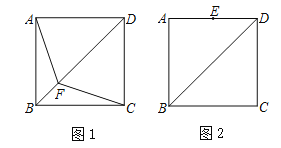
����Ŀ����֪����ͼ��������ABCD�У���F�ǶԽ���BD�ϵ�һ������.
��1����ͼ1������AF��CF��ֱ��д��AF��CF��������ϵ��
��2����ͼ2����EΪAD�ߵ��е㣬����F�˶����߶�EC��ʱ������AF��BE�ཻ�ڵ�O.
���������������ͼ2�в�ȫͼ�Σ�
�ڲ���AF��BE��λ�ù�ϵ����д��֤���˲����˼·��
����������εı߳�Ϊ2��ֱ��д��AO�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����εĶԽ��߲�һ�����е������ǣ� ��
A.����ƽ��B.���ഹֱC.ÿһ���Խ���ƽ��һ��Խ�D.���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016����ʡ�����е�23��)Ϊ����Ӧ�������У����Ŀ�꣬ijУ�ƻ�ΪѧУ����ӹ���һ��������֪����2��AƷ�Ƶ������3��BƷ�Ƶ�������380Ԫ������4��AƷ�Ƶ������2��BƷ�Ƶ�������360Ԫ��
��1����A��B����Ʒ�Ƶ�����ĵ��ۣ�
��2�����У����20��AƷ�Ƶ������2��BƷ�Ƶ�������ܷ��ã�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com