
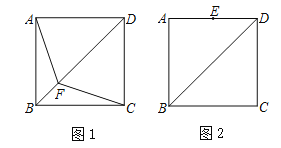
【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
【答案】(1)AF=CF(2)① 图形见解析②![]() ③
③![]() .
.
【解析】试题分析:(1)根据正方形的对称性即可得结论;(2)①根据题意,补全图形即可;②AF⊥BE,由四边形ABCD是正方形,可得AD=CD,∠ADB=∠CDB.进而可得ΔADF≌ΔCDF.从而得到1=∠2;由E为正方形ABCD的AD边的中点,可证ΔABE≌ΔDCE.从而得到∠3=∠4;由∠2+∠4=90°可知∠1+∠3=90°,进而可得∠AOE=90°,即AF⊥BE.③根据勾股定理可得BE=![]() ,因AF⊥BE,根据
,因AF⊥BE,根据![]() ,即可求得AO的长.
,即可求得AO的长.
试题解析:
(1)解:AF=CF.
(2)解:① 补全图形:
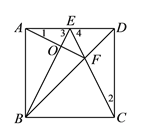
②![]() .
.
证明思路如下:
(i)由四边形ABCD是正方形,
可得AD=CD,∠ADB=∠CDB.
进而可得![]() ≌
≌![]() .从而得到1=∠2.
.从而得到1=∠2.
(ii)由E为正方形ABCD的AD边的中点,可证![]() ≌
≌![]() .
.
从而得到∠3=∠4.
(iii)由∠2+∠4=90°可知∠1+∠3=90°,进而可得∠AOE=90°.
即![]() .
.
③![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,AC=DF;
④∠A=∠D,∠B=∠E,∠C=∠F.
其中,能使△ABC≌△DEF的条件共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.

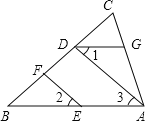
图⑴ 图⑵
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知:点![]() 在双曲线
在双曲线![]() :
:![]() 上,直线
上,直线![]() ,直线
,直线![]() 与
与![]() 关于原点成中心对称,
关于原点成中心对称,![]() 两点间的连线与曲线
两点间的连线与曲线![]() 第一象限内的交点为
第一象限内的交点为![]() ,
,![]() 是曲线
是曲线![]() 上第一象限内异于
上第一象限内异于![]() 的一动点,过
的一动点,过![]() 作
作![]() 轴平行线分别交
轴平行线分别交![]() ,
,![]() 于
于![]() 两点.
两点.
(1)求双曲线![]() 及直线
及直线![]() 的解析式;
的解析式;
(2)求证:![]() ;
;
(3)如图2所示,![]() 的内切圆与
的内切圆与![]() 三边分别相切于点
三边分别相切于点![]() ,求证:点
,求证:点![]() 与点
与点![]() 重合.(参考公式:在平面坐标系中,若有点
重合.(参考公式:在平面坐标系中,若有点![]() ,
,![]() ,则A、B两点间的距离公式为=
,则A、B两点间的距离公式为=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省泰安市第26题)某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数![]() 的图象与BC边交于点E.
的图象与BC边交于点E.
⑴当F为AB的中点时,求该函数的解析式;
⑵当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com