
如图,抛物线 与x轴交于A、B两点,与y轴交于点C.
与x轴交于A、B两点,与y轴交于点C.
(1)分别求出点A、B、C的坐标;
(2)设抛物线 的顶点为M,求四边形ABMC的面积.
的顶点为M,求四边形ABMC的面积.
(1)A(﹣1,0),B(3,0),C(0,﹣3);(2)四边形ABMC的面积是9.
解析试题分析:(1)把y=0和x=0分别代入解析式即可求出A、B、C的坐标;
(2)把解析式化成顶点式即可求出M的坐标,过M作MN⊥X轴于N,这样四边形ACMB的面积就转化成△ACO、梯形OCMN、△BMN的面积,根据点的坐标求出各个面积代入即可.
试题解析:(1)当y=0时,x2﹣2x﹣3=0,
解得:x1=3,x2=﹣1,
∴点A的坐标是(﹣1,0),点B的坐标是(3,0),
当x=0时,y=﹣3,
∴点C的坐标是(0,﹣3),
故答案为:A(﹣1,0),B(3,0),C(0,﹣3);
(2)y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴M(1,﹣4),
过M作MN⊥X轴于N,
则:ON=1,MN=4,BN=3﹣1=2,OA=1,OC=3,
∴四边形ABMC的面积S=S△COA+S梯形CONM+S△BNM,
= OA×OC+
OA×OC+ ×(OC+MN)×ON+
×(OC+MN)×ON+ ×MN×BN
×MN×BN
= ×1×3+
×1×3+ ×(3+4)×1+
×(3+4)×1+ ×2×4,
×2×4,
=9.
答:四边形ABMC的面积是9.
考点:二次函数综合题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.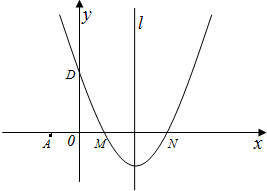
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y= x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的坐标是(1,0),点B的坐标是(﹣3,0).
x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的坐标是(1,0),点B的坐标是(﹣3,0).
(1)求m、n的值;
(2)求直线PC的解析式.
[温馨提示:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ,
, )].
)].
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲.乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式 .
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,小华的身高为 ;
(3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米, 绳子甩到最高处时超过她的头顶,请结合图像,写出t的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商店将进价为每件80元的某种商品按每件100元出售,每天可售出100件.经过市场调查,发现这种商品每件每降低1元,其销售量就可增加10件.
(1)设每件商品降低售价 元,则降价后每件利润 元,每天可售出 件(用含
元,则降价后每件利润 元,每天可售出 件(用含 的代数式表示);
的代数式表示);
(2)如果商店为了每天获得利润2160元,那么每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数 的图象经过点A(2,-3),B(-1,0).
的图象经过点A(2,-3),B(-1,0).
(1)求二次函数的解析式;
(2)观察函数图象,要使该二次函数的图象与 轴只有一个交点,应把图象沿
轴只有一个交点,应把图象沿 轴向上平移几个单位?
轴向上平移几个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,已知抛物线 交
交 轴于A(2,0),B(6,0)两点,交
轴于A(2,0),B(6,0)两点,交 轴于点C(0,
轴于点C(0,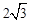 ).
).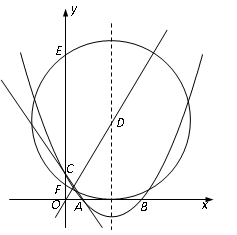
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线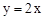 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交 轴于点E、F两点,求劣弧EF所对圆心角的度数;
轴于点E、F两点,求劣弧EF所对圆心角的度数;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,二次函数y=-x2+(m-1)x+4m的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1).
(1)求m的值及点A的坐标;
(2)如图,将△AEO沿x轴向右平移得到△A′E′O′,连结A′B、BE′.
①当点E′落在该二次函数的图象上时,求AA′的长;
②设AA′=n,其中0<n<2,试用含n的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
③当A′B+BE′取得最小值时,求点E′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com