
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲.乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式 .
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,小华的身高为 ;
(3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米, 绳子甩到最高处时超过她的头顶,请结合图像,写出t的取值范围 .
(1)抛物线的解析式是y=﹣0.1x2+0.6x+0.9;(2)小华的身高是1.8米;(3)1<t<5.
解析试题分析:(1)已知抛物线解析式,求其中的待定系数,选定抛物线上两点E(1,1.4),B(6,0.9)坐标代入即可;
(2)小华站在OD之间,且离点O的距离为3米,即OF=3,求当x=3时,函数值;
(3)实质上就是求y=1.4时,对应的x的两个值,就是t的取值范围.
试题解析:(1)由题意得点E(1,1.4),B(6,0.9),代入y=ax2+bx+0.9得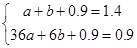 ,
,
解得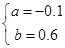 ,
,
∴所求的抛物线的解析式是y=﹣0.1x2+0.6x+0.9;
(2)把x=3代入y=﹣0.1x2+0.6x+0.9得
y=﹣0.1×32+0.6×3+0.9=1.8
∴小华的身高是1.8米;
(3)当y=1.4时,﹣0.1x2+0.6x+0.9=1.4,
解得x1=1,x2=5,
∴1<t<5.
考点:二次函数的应用.


科目:初中数学 来源: 题型:解答题
某商店经销一种销售成本为每千克40元的水产品.根据市场分析,若按每千克50元销售,一个月能销售500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x之间的函数关系式;
(3)商店想在月销售成本不超过10 000元的情况下,使得月销售利润达到5 000元,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)已知二次函数 ,请你化成
,请你化成 的形式,并在直角坐标系中画出
的形式,并在直角坐标系中画出 的图象;
的图象;
(2)如果 ,
, 是(1)中图象上的两点,且
是(1)中图象上的两点,且 ,请直接写出
,请直接写出 、
、 的大小关系;
的大小关系;
(3)利用(1)中的图象表示出方程 的根来,要求保留画图痕迹,说明结果.
的根来,要求保留画图痕迹,说明结果.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),与x轴正半轴交于点B.
(1)求这条抛物线的函数关系式;
(2)在抛物线对称轴上确定一点C,使△ABC是等腰三角形,求出所有点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图是一座古拱桥的截面图.在水平面上取点为原点,以水平面为 轴建立直角坐标系,桥洞上沿形状恰好是抛物线
轴建立直角坐标系,桥洞上沿形状恰好是抛物线 的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.
的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,抛物线 的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
(1)求抛物线的解析式;
(2)若点D′恰好落在 轴上的点(0,6)时,求此时D点的坐标;
轴上的点(0,6)时,求此时D点的坐标;
(3)直线CD′交对称轴AB于点F,
①当点D′在对称轴AB的左侧时,且△ED′F∽△CDE,求出DE:DC的值;
②连结B D′,是否存在点E,使△E D′B为等腰三角形?若存在,请直接写出BE:BC的值,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com