
分析 (1)根据有理数的乘法和加减法可以解答本题;
(2)根据乘法分配律可以解答本题;
(3)根据幂的乘方、有理数的乘除法和加减法可以解答本题;
(4)根据有理数的乘除法和减法可以解答本题.
解答 解:(1)(-10)+8×(-2)-(-4)×(-3)
=(-10)+(-16)-12
=-38;
(2)36×($\frac{1}{4}$-$\frac{1}{9}$-$\frac{1}{12}$)
=$36×\frac{1}{4}-36×\frac{1}{9}-36×\frac{1}{12}$
=9-4-3
=2;
(3)-22÷$\frac{4}{3}$-[22-(1-$\frac{1}{2}$×$\frac{1}{3}$)]×12
=-4×$\frac{3}{4}-[4-(1-\frac{1}{6})]×12$
=-3-[4-$\frac{5}{6}$]×12
=-3-4×12+$\frac{5}{6}$×12
=-3-48+10
=-41;
(4)3$\frac{3}{8}$×(8$\frac{1}{3}$-3$\frac{1}{8}$)÷1$\frac{1}{24}$×$\frac{8}{27}$
=$\frac{27}{8}×\frac{125}{24}×\frac{24}{25}×\frac{8}{27}$
=5.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
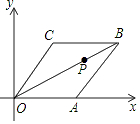 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为($\frac{10}{7}$,$\frac{5}{7}$).
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为($\frac{10}{7}$,$\frac{5}{7}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
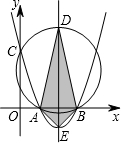 如图,开口向上的抛物线y=$\frac{1}{a}$(x-a)(x-3a)的顶点为E,与x轴相交于点A、B两点,与y轴交于点C,经过A、B、C三点的圆与抛物线的对称轴在x轴上方的交点为D.已知圆的半径是$3\sqrt{5}$,则四边形AEBD的面积是27+9$\sqrt{5}$.
如图,开口向上的抛物线y=$\frac{1}{a}$(x-a)(x-3a)的顶点为E,与x轴相交于点A、B两点,与y轴交于点C,经过A、B、C三点的圆与抛物线的对称轴在x轴上方的交点为D.已知圆的半径是$3\sqrt{5}$,则四边形AEBD的面积是27+9$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com