
分析 (1)根据有理数的加减法可以解答本题;
(2)根据有理数的乘除法可以解答本题;
(3)根据幂的乘方、有理数的乘除法和减法可以解答本题.
解答 解:(1)24-|-2|+(-16)-8
=24-2-16-8
=-2;
(2)(-2)×$\frac{3}{2}$÷(-$\frac{3}{4}$)×4
=2×$\frac{3}{2}×\frac{4}{3}×4$
=16;
(3)-12016-(1-0.5)÷3×[2-(-3)2]
=-1-$\frac{1}{2}×\frac{1}{3}×[2-9]$
=-1-$\frac{1}{2}×\frac{1}{3}×(-7)$
=-1+$\frac{7}{6}$
=$\frac{1}{6}$.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
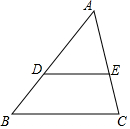 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,DB=2,则$\frac{DE}{BC}$的值等于$\frac{3}{5}$.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,DB=2,则$\frac{DE}{BC}$的值等于$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com