练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：(1)(－)－(＋)；　　　　　　　　　(2)(＋3.7)－(＋6.8)；

    (3)(－16)－(－10)； (4)3.36－4.16.

    【答案】(1)－；(2)－3.1；(3)－5；(4)－0.8.

    【解析】

    （1）（2）（3）（4）均考查有理数的减法法则：减去一个数等于加上这个数的相反数，原式利用减法法则变形和计算即可得到结果.

    (1)(－)－(＋)= －－=－()＝－；

    (2)(＋3.7)－(＋6.8)＝3.7－6.8＝－(6.8－3.7)=－3.1；

    (3)(－16)－(－10)= －16+10=－(－)=－5；

    (4)3.36－4.16＝－(4.16－3.36)=－0.8.

    故答案为(1)－；(2)－3.1；(3)－5；(4)－0.8.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某制造企业有一座对生产设备进行水循环冷却的冷却塔，冷却塔的顶部有一个进水口，3小时恰好可以注满这座空塔，底部有一个出水口，7小时恰好可以放完满塔的水．为了保证安全，塔内剩余水量不得少于全塔水量的 ，出水口一直打开，保证水的循环，进水口根据水位情况定时对冷却塔进行补水．假设每次恰好在剩余水量为满水量的m倍时开始补水，补满后关闭进水口．
    （1）当m= 时，请问：两次补水之间相隔多长时间？每次补水需要多长时间？
    （2）能否找到适当的m值，使得两次补水的间隔时间和每次的补水时间一样长？如果能，请求出m值；如果不能，请你分析两次补水的间隔时间和每次的补水时间之间的数量关系，并表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在已知的ABC中，按以下步骤作图：
    ①分别以B，C为圆心，以大于 BC的长为半径作弧，两弧相交于两点M，N；
    ②作直线MN交AB于点D，连接CD.若CD=AC，∠A=50°，则∠ACB的度数为（ ）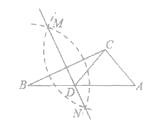

    A.90°
    B.95°
    C.100°
    D.105°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点.

    （1）求AD的长及抛物线的解析式；
    （2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动，设运动时间为t秒，当t为何值时，以P，Q，C为顶点的三角形与ADE相似？
    （3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把几个数用大括号括起来，中间用逗号断开，如：{1，2，－3}，{－2，7，，19}，我们称之为集合，其中的数称为集合的元素．如果一个集合满足：当有理数a是集合的元素时，有理数5－a也必是这个集合的元素，这样的集合我们称为好的集合．例如集合{5，0}就是一个好的集合．

    (1)请你判断集合{1，2}，{－2，1，2.5，4，7}是不是好的集合？

    (2)请你再写出两个好的集合(不得与上面出现过的集合重复)；

    (3)写出所有好的集合中，元素个数最少的集合．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一天，龟、兔进行了600米赛跑，如图表示龟兔赛跑的路程s(米)与时间t(分钟)的关系(兔子睡觉前后速度保持不变)，根据图象回答以下问题：

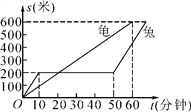
    (1)赛跑中，兔子共睡了多少时间？

    (2)赛跑开始后，乌龟在第几分钟时从睡觉的兔子旁经过？

    (3)兔子跑到终点时，乌龟已经到了多长时间？并求兔子赛跑的平均速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

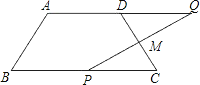
    【题目】如图，在四边形ABCD中，AD∥BC，AD=5cm，BC=9cm．M是CD的中点，P是BC边上的一动点（P与B，C不重合），连接PM并延长交AD的延长线于Q．

    （1）试说明△PCM≌△QDM．

    （2）当点P在点B、C之间运动到什么位置时，四边形ABPQ是平行四边形？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1.纸上有5个边长为1的小正方形组成的纸片，可把它剪拼成一个正方形（图2）

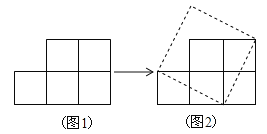
    （图3）

    拼成的正方体的面积与边长分别是多少？

    你能把这十个小正方体组成的图形纸（图3），剪拼成一个大正方形吗？若能，则请画出剪拼成的大正方形，并求出其边长为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，方格纸中每一个小方格的边长为1个单位，试解答下列问题：

    的顶点都在方格纸的格点上，先将向右平移2个单位，再向上平移3个单位，得到，其中点、、分别是A，B、C的对应点，试画出．

    连接、，则线段、的位置关系为______，线段、的数量关系为______；

    平移过程中，线段AB扫过部分的面积为______平方单位

    查看答案和解析>>

    同步练习册答案