
【题目】如图,直线![]() 与x,y轴分别交于点A,B,与反比例函数
与x,y轴分别交于点A,B,与反比例函数![]() (k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
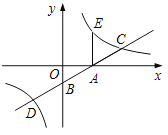
(1)求点A的坐标.
(2)若AE=AC.
①求k的值.
②试判断点E与点D是否关于原点O成中心对称?并说明理由.
【答案】(1)(3,0);(2)①k=6,②点E与点D关于原点O成中心对称.
【解析】
试题分析:(1)令y=0,可求得x=3,因此A点坐标为(3,0);(2)①易知∠CAF=30°,而AE=AC,因此可用AE表示AF,CF,从而点C的坐标可以表示出来,再代到反比例函数解析式中可以求得AE长度,k值也就可求.②利用反比例函数解析式和一次函数解析式可求得点D坐标,即可判断.
试题解析:(1)当y=0时,得0=![]() x-
x-![]() ,解得x=3.∴点A的坐标为(3,0).
,解得x=3.∴点A的坐标为(3,0).
(2)①过点C作CF⊥x轴于点F.设AE=AC=t, 点E的坐标是(3,t).在Rt△AOB中, tan∠OAB=![]() ,∴∠OAB=30°.在Rt△ACF中,∠CAF=30°, ∴CF=t,AF=AC·cos30°=
,∴∠OAB=30°.在Rt△ACF中,∠CAF=30°, ∴CF=t,AF=AC·cos30°=![]() t,∴点C的坐标是
t,∴点C的坐标是 .∴
.∴ , 解得t1=0(舍去),t2=2.所以,k=3t=6. ②点E的坐标为(3,2
, 解得t1=0(舍去),t2=2.所以,k=3t=6. ②点E的坐标为(3,2![]() ), 设点D的坐标是(
), 设点D的坐标是(![]() ), ∴x(
), ∴x(![]() )=6,解得x1=6,x2=-3, ∴点D的坐标是(-3,-2),所以,点E与点D关于原点O成中心对称.
)=6,解得x1=6,x2=-3, ∴点D的坐标是(-3,-2),所以,点E与点D关于原点O成中心对称.



科目:初中数学 来源: 题型:
【题目】某校八年级(二)班5位女生的体重(单位:kg)分别是:36,37,39,41,41. 则这组数据的中位数是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是______米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是______ 米.
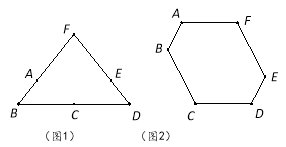
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2017个格子中的数为( )
3 | a | b | c | ﹣1 | 2 | … |
A. 3 B. 2 C. 0 D. ﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新运算:a*b=a2﹣b+ab.例如:1*2=12﹣2+1×2=1
(1)求2*(﹣3)的值.
(2)求(﹣2)*[2*(﹣3)]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com