
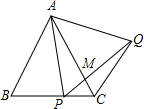
 如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )| A. | ①② | B. | ①③ | C. | ①②③ | D. | ①②③④ |
分析 根据等边三角形性质得出AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,求出∠BAP=∠CAQ,根据SAS证△ABP≌△ACQ,推出∠ACQ=∠B=60°=∠BAC,根据平行线的判定推出即可,再根据等腰三角形性质求出∠BAP=30°,求出∠PMA=90°,即可得出答案.
解答 证明:如图,∵△ABC和△APQ是等边三角形,
∴AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,
∴∠BAP=∠CAQ=60°-∠PAC,
在△ABP和△ACQ中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAP=∠CAQ}\\{AP=AQ}\end{array}\right.$,
∴△ABP≌△ACQ(SAS),
∴∠ACQ=∠B=60°=∠BAC,故②正确,
∴AB∥CQ,故①正确,
∵∠APQ=∠ACQ=60°,∠PAC=∠PAC,
∴△APM∽△ACP,
∴$\frac{AP}{AC}$=$\frac{AM}{AP}$,
∴AP2=AC•AM,故③正确,
∵BP=PC,
∴∠BAP=30°,
∴∠PAC=30°,
∵∠APM=60°,
∴∠AMP=90°,
∴PQ⊥AC,故④正确.
故选:D.
点评 本题考查了相似三角形的判定和性质,等边三角形性质,全等三角形的性质和判定,平行线性质和判定,等腰三角形性质的应用,主要考查学生的推理能力.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
| 港口 | 从甲仓库运(吨) | 从乙仓库运(吨) |
| A港 | x | 100-x |
| B港 | 80-x | x-30 |
| 港口 | 从甲仓库运到港口费用(元) | 从乙仓库运到港口费用(元) |
| A港 | 14x | 20(100-x) |
| B港 | 10(80-x) | 8(x-30) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
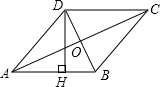 如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为( )
如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为( )| A. | 4.8cm | B. | 5cm | C. | 9.6cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
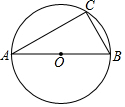 如图,⊙O是△ABC的外接圆,∠C=90°,sin∠A=$\frac{\sqrt{3}}{3}$,BC=2$\sqrt{3}$,则⊙O的半径为3.
如图,⊙O是△ABC的外接圆,∠C=90°,sin∠A=$\frac{\sqrt{3}}{3}$,BC=2$\sqrt{3}$,则⊙O的半径为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
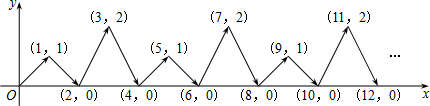
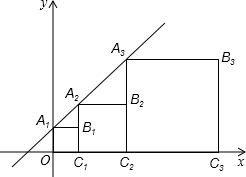 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1,B2,B3,B4的坐标分别为(1,1)(3,2),(7,4),(15,8),则Bn的坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1,B2,B3,B4的坐标分别为(1,1)(3,2),(7,4),(15,8),则Bn的坐标是( )| A. | (2n-1,2n-1) | B. | (2n,2n-1) | C. | (2n-1,2n) | D. | (2n-1-1,2n-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com