
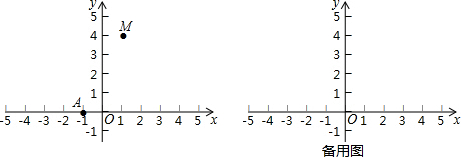
分析 分两种情形讨论①当AM是矩形的一条边时,如图1所示.②当AM是对角线时,AQ⊥MQ时,PQ与y轴重合,如图2所示,根据相似三角形或全等三角形的性质即可解决问题.
解答 解:∵点M(1,4),点A(-1,0),
∴AM=2$\sqrt{5}$,线段AM中点N(0,2),
∴AN=MN=$\sqrt{5}$,
①当AM是矩形的一条边时,分别过M、A作直线l1⊥AM交y轴于P1;l2⊥AM交y轴于P2,如图1所示.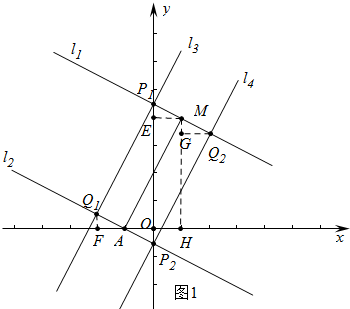
过P1作l3∥AM交l2于Q1,过P2作直线l4交l1于Q2,作ME⊥y轴于E,MH⊥x轴于H,作Q1F⊥x轴于F,Q2G⊥MH于G,
则ON=EN=2,OA=ME,
∵∠P1EM=∠MEN,∠MP1E=∠EMN,
∴△P1EM∽△MEN,
∴$\frac{{P}_{1}E}{ME}=\frac{ME}{EN}$,
∴$\frac{{P}_{1}E}{1}$=$\frac{1}{2}$,
∴P1E=$\frac{1}{2}$,在△P1EM和△Q1FA中,
$\left\{\begin{array}{l}{∠{P}_{1}EM=∠{Q}_{1}FA}\\{∠{P}_{1}ME=∠{Q}_{1}AF}\\{{P}_{1}M=A{Q}_{1}}\end{array}\right.$
∵△P1EM≌△Q1FA,
∴Q1F=P1E=$\frac{1}{2}$,AF=EM=1,
∴OF=OA+AF=2,
∴Q1(-2,$\frac{1}{2}$),
同理△Q2MG≌△AOP2≌△AON,可得MG=OP2=$\frac{1}{2}$,Q2G=OA=1,
∴GH=4-$\frac{1}{2}$=$\frac{7}{2}$,∴Q2(2,$\frac{7}{2}$),
②当AM是对角线时,AQ⊥MQ时,PQ与y轴重合,如图2所示,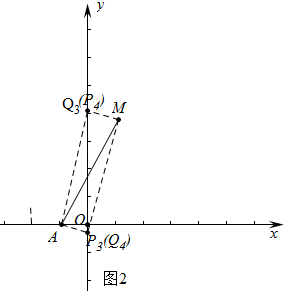
∵AQ2+MQ2=AM2,设Q(0,m),
∴AQ2=m2+1,MQ2=(m-4)2+12=m2-8m+17,
∴(m2+1)+(m2-8m+17)=20,
整理得m2-4m-1=0,解得m1=2+$\sqrt{5}$,m2=2-$\sqrt{5}$,
∴Q3(0,2+$\sqrt{5}$),Q4(0,2-$\sqrt{5}$).
综上所述出点Q的坐标为:Q1(-2,$\frac{1}{2}$),Q2(2,$\frac{7}{2}$),Q3(0,2+$\sqrt{5}$),Q4(0,2-$\sqrt{5}$).
点评 本题考查矩形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质、坐标与图形的性质等知识,解题的关键是学会分类讨论,需要正确画出图形,综合性比较强,属于中考压轴题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批圆珠笔的寿命 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 检查一枚用于发射卫星的运载火箭的各零部件 | |
| D. | 考察人们保护海洋的意识 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
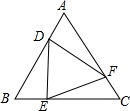 如图,等边△ABC中,点D、E、F分别同时从点A、B、C出发,以相同的速度在AB、BC、CA上运动,连结DE、EF、DF.
如图,等边△ABC中,点D、E、F分别同时从点A、B、C出发,以相同的速度在AB、BC、CA上运动,连结DE、EF、DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com