
【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有![]() x2+x≥﹣
x2+x≥﹣![]() ;④在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣
;④在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣![]() ,其中结论错误的是 (只填写序号).
,其中结论错误的是 (只填写序号).
【答案】②.
【解析】
试题分析:根据题意,可得二次函数图象如图,

由图象可得a<0.b<0,c>0,所以abc>0,①正确.由a+b+c=0可得c=﹣a﹣b,所以a+3b+2c=a+3b﹣2a﹣2b=b﹣a,又因x=﹣1时,y>0,即a﹣b+c>0,所以b﹣a<c,再由c>0,可判定b﹣a可以是正数,所以a+3b+2c≤0,②错误.因函数y′=![]() ,由
,由![]() >0,可得函数y′有最小值﹣
>0,可得函数y′有最小值﹣![]() ,所以
,所以![]() x2+x≥﹣
x2+x≥﹣![]() ,③正确.已知y=ax2+bx+c的图象经过点(1,0),可得a+b+c=0,即c=﹣a﹣b,令y=0则ax2+bx﹣a﹣b=0,设它的两个根为x1,1,根据根与系数的关系可得
,③正确.已知y=ax2+bx+c的图象经过点(1,0),可得a+b+c=0,即c=﹣a﹣b,令y=0则ax2+bx﹣a﹣b=0,设它的两个根为x1,1,根据根与系数的关系可得
x11=![]() ,即x1=
,即x1=![]() ,又因﹣2<x1<x2,所以在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣
,又因﹣2<x1<x2,所以在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣![]() ,④正确.
,④正确.


科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
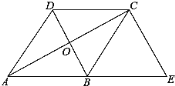
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com