Question

【题目】如图，在正方形ABCD中，E是对角线BD上一点，且满足BE=BC．连接CE并延长交AD于点F，连接AE，过B点作BG⊥AE于点G，延长BG交AD于点H．在下列结论中：

①AH=DF； ②∠AEF=45°； ③S四边形EFHG=S△DEF+S△AGH，

其中正确的结论有_____________________．(填正确的序号)

Answer 1

【答案】①②

【解析】∵BD是正方形ABCD的对角线，

∴∠ABE=∠ADE=∠CDE=45，AB=BC，

∵BE=BC，

∴AB=BE，

∵BG⊥AE，

∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5，

在Rt△ABH中,∠AHB=90∠ABH=67.5，

∵∠AGH=90，

∴∠DAE=∠ABH=22.5，

在△ADE和△CDE中， ，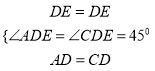

∴△ADE≌△CDE，

∴∠DAE=∠DCE=22.5，

∴∠ABH=∠DCF，

在Rt△ABH和Rt△DCF中， ，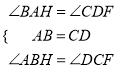

∴Rt△ABH≌Rt△DCF，

∴AH=DF,∠CFD=∠AHB=67.5，

∵∠CFD=∠EAF+∠AEF，

∴67.5=22.5+∠AEF，

∴∠AEF=45，故①②正确；

如图，连接HE，

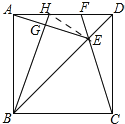
∵BH是AE垂直平分线，

∴AG=EG

∴S△AGH=S△HEG，

∵AH=HE，

∴∠AHG=∠EHG=67.5，

∴∠DHE=45，

∵∠ADE=45，

∴∠DEH=90,∠DHE=∠HDE=45，

∴EH=ED，

∴△DEH是等腰直角三角形，

∵EF不垂直DH，

∴FH≠FD，

∴S△EFH≠S△EFD，

∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH，故③错误，

∴正确的是①②.