
分析 分三种情讨论即可①如图1中,当AE=AF,EF=2$\sqrt{2}$时.②如图2中,当AE=AF,EF=2$\sqrt{2}$时.③如图3中,当FA=EF,AE=2$\sqrt{2}$时.
解答 解:①如图1中,当AE=AF,EF=2$\sqrt{2}$时,易知AE=AF=2.
②如图2中,当AE=AF,EF=2$\sqrt{2}$时,CE=CF=2,BE=DF=1,AE=AF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.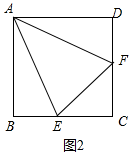
③如图3中,当FA=EF,AE=2$\sqrt{2}$时,作FG⊥AE于G,则四边形AGFD是矩形,AD=FG=3,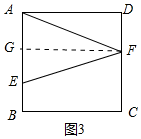
∵FA=FE,FG⊥AE,
∴AG=$\sqrt{2}$,
在Rt△AFG中,AF=EF=$\sqrt{(\sqrt{2})^{2}+{3}^{2}}$=$\sqrt{11}$,
综上所述,腰三角形AEF的腰长是2或$\sqrt{10}$或$\sqrt{11}$.
故答案为2或$\sqrt{10}$或$\sqrt{11}$.
点评 本题考查正方形的性质、等腰三角形的判定和性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
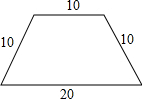 有一根围成梯形的篱笆,它的各边长如图所示,为了其他用处,将它改围成一个长方形篱笆,使得围成的长方形的一边长为10,则此时篱笆围成的长方形的另一边长为多少?若改围成一个正方形的篱笆,正方形的边长为多少?并比较围出的长方形和正方形哪个面积更大?
有一根围成梯形的篱笆,它的各边长如图所示,为了其他用处,将它改围成一个长方形篱笆,使得围成的长方形的一边长为10,则此时篱笆围成的长方形的另一边长为多少?若改围成一个正方形的篱笆,正方形的边长为多少?并比较围出的长方形和正方形哪个面积更大?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
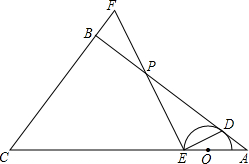 如图,在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,连接ED,过点E作ED的高,交射线AB于点P,交射线CB于点F.
如图,在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,连接ED,过点E作ED的高,交射线AB于点P,交射线CB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com