
某商店经营一种成本为每千克40美元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,
(1)针对这种水产品的销售情况,设销售单价定为x元(x>50),
请用的x代数式表示月销售量, 以及获得的利润.
(2)当x取什么数时利润最大? 最大利润是多少?
科目:初中数学 来源: 题型:
如图,⊙M与x轴交于A、B两点,其坐标分别为 、
、 ,直径CD⊥x轴于N,抛物线
,直径CD⊥x轴于N,抛物线 经过A、B、D三点,
经过A、B、D三点,
(1) 求m的值及点D的坐标.
(2)若直线CE切⊙M于点C,G在直线CE上,已知点G的横坐标为3. 求G的纵坐标
(3) 对于(2)中的G,是否存在过点G的直线,使它与(1)中抛物 线只有一个交点,请说明理由
线只有一个交点,请说明理由 .
.
(4) 对于(2)中的G 直线FG切⊙M于
 点F,求直线DF的解析式.
点F,求直线DF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线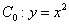 ,顶点记作
,顶点记作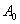 .首先我们将抛物线
.首先我们将抛物线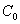 关于直线
关于直线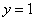 对称翻折过去得到抛物线
对称翻折过去得到抛物线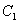 称为第一次操作,再将抛物线
称为第一次操作,再将抛物线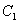 关于直线
关于直线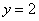 对称翻折过去得到抛物线
对称翻折过去得到抛物线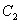 称为第二次操作,…,将抛物线
称为第二次操作,…,将抛物线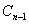 关于直线
关于直线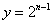 对称翻折过去得到抛物线
对称翻折过去得到抛物线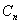 (顶点记作
(顶点记作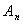 )称为第n此操作(n=1,2,3…),….设抛物线
)称为第n此操作(n=1,2,3…),….设抛物线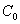 与抛物线
与抛物线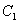 交于两点
交于两点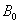 与
与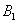 ,顺次连接
,顺次连接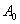 、
、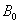 、
、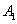 、
、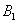 四个点得到四边形
四个点得到四边形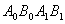 ,抛物线
,抛物线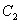 与抛物线
与抛物线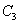 交于两点
交于两点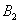 与
与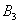 ,顺次连接
,顺次连接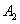 、
、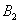 、
、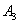 、
、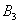 四个点得到四边形
四个点得到四边形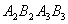 ,…,抛物线
,…,抛物线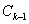 与抛物线
与抛物线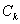 交于两点
交于两点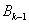 与
与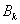 ,顺次连接
,顺次连接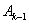 、
、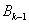 、
、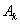 、
、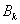 四个点得到四边形
四个点得到四边形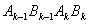 (k=1,3,5…),….
(k=1,3,5…),….
(1)请分别直接写出抛物线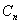 (n=1,2,3,4)的解析式;
(n=1,2,3,4)的解析式;
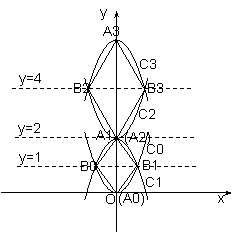 (2)一系列四边形
(2)一系列四边形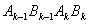 (k=1,3,5…)
(k=1,3,5…)
为哪种特殊的四边形(说明理由)?它们
都相似吗?如果全都相似,请证明之;如
果不全都相似,请举出一对不相似的反例;
(3)试归纳出抛物线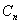 的解析式,无需证明.
的解析式,无需证明.
并利用你归纳出来的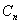 的解析式
的解析式
求四边形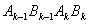 (k=1,3,5…)
(k=1,3,5…)
的面积(用含k的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com