
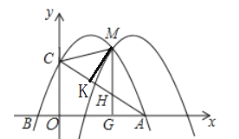
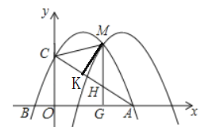
����Ŀ����ͼ��������y��ax2+bx+2��a��0����x�ύ��A��4��0����B����1��0�����㣬��y�ύ�ڵ�C��
��1���������ߵı���ʽ�Ͷ������ꣻ
��2���ѣ�1�����������������ΪC1����C1����ƽ��m����λ�õ�������C2��C1��C2���ڵ�һ������ΪM������M��MK![]() ��K��MG��x���ڵ�G�����߶�AC�ڵ�H������CM��
��K��MG��x���ڵ�G�����߶�AC�ڵ�H������CM��
�����߶�MK���ȵ����ֵ��
������CMHΪ����������ʱ��������������ƽ�Ƶľ���m�ʹ�ʱ��M�����꣮
���𰸡���1��![]() ��(
��(![]() ��2����
��2����![]() ����m��1ʱ��M��2��3������m��5��2
����m��1ʱ��M��2��3������m��5��2![]() ʱ��M
ʱ��M![]() ��
��
��������
��1�����õ�A��B������õ������ߵĽ���ʽ�������������ɶ���ʽ�����ɵö������ꣻ
��2���ٹؼ���֤��![]() ��
��![]() �õ�MK=
�õ�MK=![]() ����бΪֱ��ֻ��MH�������ʱ��MK���������M(x����
����бΪֱ��ֻ��MH�������ʱ��MK���������M(x����![]() x2+
x2+![]() +2��,H(x����
+2��,H(x����![]() x+2����MH���ȵ����ֵת��Ϊ���κ�������ֵ���⼴����⣻
x+2����MH���ȵ����ֵת��Ϊ���κ�������ֵ���⼴����⣻
����CMHΪ���������Σ��������������������CM��CHʱ����ii����HC��HMʱ,��iii����CM��HMʱ���ֱ���������Ӧ�ļ������������������õ���M�����꣬����ƽ�ƺ�Ľ���ʽ�����m��ֵ��
�⣺��1����x��0ʱ��y��ax2+bx+2��2��
�������߾�����0��2����
��������y��ax2+bx+2��a��0����x�ύ��A��4��0����B����1��0�����㣬
�������ߵı���ʽΪ��y��a��x��4����x+1����
�ѣ�0��2������ã�2��a��0��4����0+1����
a����![]() ��
��
��y����![]() ��x��4����x+1������
��x��4����x+1������![]() x2+
x2+![]() +2����
+2����![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
�������ߵı���ʽΪ��![]() ������������(
������������(![]()
(2)����ֱ��AC�ı���ʽΪ��y��kx+b��
��A��4��0����C��0��2������ã�![]() ��
��
��ã�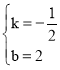 ��
��
��ֱ��AC�Ľ���ʽΪ��y����![]() x+2��
x+2��
![]()
![]() ��
��
![]()
![]() ��
��![]() ��
��
![]()
![]()
![]() ��
��
��M(x����![]() x2+
x2+![]() +2��,H(x����
+2��,H(x����![]() x+2������֪
x+2������֪![]()
![]() MK=
MK=![]() =
=![]() [��
[��![]() x2+
x2+![]() +2-(��
+2-(��![]() x+2)]=
x+2)]=![]() [-
[-![]() ]
]
��x=2ʱ��MK������![]()
�ڡߡ�CMHΪ���������Σ������������
��������CM��CHʱ��C��MH��ֱƽ�����ϵĵ㣬����C��CP��MH����MP=PH��
����ͼ��֪OC=PG=2
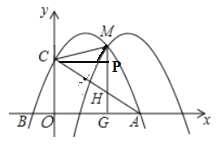
��GH+GM=PG-PH+PG+MP=2PG=2OC
��GH+GM��4��
��![]() x2+
x2+![]() +2+����
+2+����![]() x+2����4����ã�x1��0���ᣩ��x2��2��
x+2����4����ã�x1��0���ᣩ��x2��2��
��M��2��3����
��ƽ�ƺ�������ߵı���ʽΪ��y����![]() ��x��
��x��![]() ��m��2+
��m��2+![]() ��
��
��M��2��3������ã�m��1��
��������HC��HMʱ��HM����![]() x2+
x2+![]() x+2������
x+2������![]() x+2������
x+2������![]() x2+2x��
x2+2x��
CH2��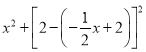 ��CH��
��CH��![]() ��
��
��![]() ����
����![]() x2+2x�����x1��0���ᣩ��x2��4��
x2+2x�����x1��0���ᣩ��x2��4��![]() ��
��
��M��4��![]() ����
����![]() ����
����
��ƽ�ƺ�������ߵı���ʽΪ��y����![]() ��x��
��x��![]() ��m��2+
��m��2+![]() ��
��
��M��4��![]() ����
����![]() ������ã�m1��0���ᣩ��m2��5��2
������ã�m1��0���ᣩ��m2��5��2![]() ��
��
��������CM��HMʱ��HM����![]() x2+2x��CM2��
x2+2x��CM2��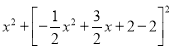 ��
��
��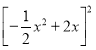 ��
��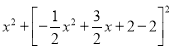 �� ���x��
�� ���x��![]() ��
��
��M��![]() ��
��![]() ����
����
��ƽ�ƺ�������ߵı���ʽΪ��y����![]() ��x��
��x��![]() ��m��2+
��m��2+![]() ��
��
��M��![]() ��
��![]() ������ã�m��0���ᣩ��
������ã�m��0���ᣩ��
������������m��1ʱ��M��2��3������m��5��2![]() ʱ��M��4��
ʱ��M��4��![]() ����
����![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬AB=BC=![]() ������ABC�Ƶ�C��ʱ����ת60�㣬�õ���MNC������AN����AN�ij���____��
������ABC�Ƶ�C��ʱ����ת60�㣬�õ���MNC������AN����AN�ij���____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
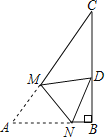
����Ŀ����ͼ����֪Rt��ABC�У���B��90�㣬��A��60�㣬AB��3����M��N�ֱ����߶�AC��AB�ϣ�����ANM��ֱ��MN�۵���ʹ��A�Ķ�Ӧ��Dǡ�������߶�BC�ϣ�����DCMΪֱ��������ʱ����AM�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
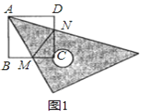
����Ŀ����֪������ABCD��һ����ֱ�����ǰ��һ����Ƕ�����A�غϣ��������ǰ���A����תʱ�����߷ֱ�ֱ��BC��CD��M��N.
��1����M��N�ֱ��ڱ�BC��CD��ʱ����ͼ1������֤��BM+DN=MN��
��2����M��N�ֱ��ڱ�BC��CD���ڵ�ֱ����ʱ����ͼ2��ͼ3�����߶�BM��DN��MN֮������������������ϵ����ֱ��д�����ۣ�
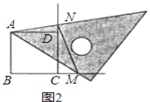
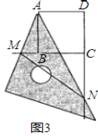
��3����ͼ3�У���ֱ��BD��ֱ��AM��AN��P��Q���㣬��MN=10��CM=8����AP�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ.����ͼ���е������Ǽף��ң�������У�����Աÿ��10�ε�����Եijɼ�.���Թ���Ϊÿ����������10����ÿ����λ1����1��.

(1)���˶�Ա�����Գɼ���ƽ��������������7����ɼ�ͳ�Ʊ���a= ,b= ��
(2)����������Ա��ѡ��һλ����ɼ������ҽ�Ϊ�ȶ���ͬѧ��Ϊ��������������ˣ�����Ϊѡ˭�����ʣ���������ѧ����ͳ�������Է���˵��(�ο����ݣ����˳ɼ��ķ���ֱ�Ϊ![]() ��
��![]() ��
��![]() )
)
(3)ѵ���ڼ�ס��ҡ�������֮��������������Ϸ�����ɼ״����������δ�����ص������еĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC=1����BAC=45�㣬��AEF���ɡ�ABC�Ƶ�A��˳ʱ�뷽����ת�õ���.����BE��CF�ཻ�ڵ�D.
��1����֤��BE=CF.
��2�����ı���ACDEΪ����ʱ����BD�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
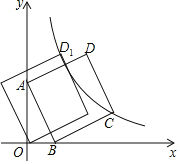
����Ŀ����ͼ��ֱ��AB��x�������ύ�ڵ�B����B��1��0������y�������ύ�ڵ�A�����߶�ABΪ�ߣ��ڵ�һ��������������ABCD����C����˫����y��![]() ��k��0���ϣ���������ABCD��x�Ḻ����ƽ��2����λ���ȣ�ʹ��Dǡ������˫����y��
��k��0���ϣ���������ABCD��x�Ḻ����ƽ��2����λ���ȣ�ʹ��Dǡ������˫����y��![]() ��k��0���ϵĵ�D1������k��_____��
��k��0���ϵĵ�D1������k��_____��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
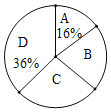
����Ŀ��2020��4�����ҹ���32�����������£�ijУ���꼶ͨ�����ξ���������Ϊ���������ң�����ͬ������֪ʶ�������Ϊ�˽�ȫ�꼶500��ѧ���˴ξ����ɼ����ٷ��ƣ�������������ȡ�˲��ֲ���ѧ���ijɼ������������Ƴ����²�������ͳ�Ʊ�����1����ͳ��ͼ����ͼ���������ͼ����Ϣ����������⣺
��1�����ε���һ�������ȡ��____������ѧ���ijɼ���
��2����1��a��__��
��3������ȡ�IJ���ѧ���ijɼ�����λ�����ڵ��������__��
��4��ͳ��ͼ��B����ռ�İٷֱ���_______��
��5��������ƣ���У���꼶�����ɼ��ﵽ80�����ϣ���80�֣���ѧ��������
��1 ֪ʶ�����ɼ�����ͳ�Ʊ�
��� | ����/�� | Ƶ�� |
A | 60��x��70 | a |
B | 70��x��80 | 10 |
C | 80��x��90 | 14 |
D | 90��x��100 | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���շ��ź���ѳ�Ϊ������Ⱥ���н�����ϵ����ǿ�����һ���֣����������������˫��̥��������һ��ͯ���ڼ�ĶԻ���
���ʣ���1��2015�굽2017�����������������һ�յ���������������Ƕ��٣�
��2��2017����һ����������ø��յ��˶���Ǯ���ź����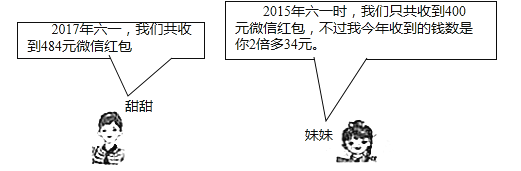
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com