
【题目】如图,在菱形ABCD中,∠A=110°,E , F分别是边AB和BC的中点,EP⊥CD于点P , 求∠FPC . 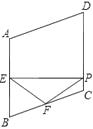
【答案】解答:解:延长PF交AB的延长线于点G , ,在△BGF与△CPF中, 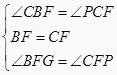 ,∴△BGF≌△CPF , ∴GF=PF , ∴F为PG中点.又∵EP⊥CD , ∴∠BEP=90°,∴EF=
,∴△BGF≌△CPF , ∴GF=PF , ∴F为PG中点.又∵EP⊥CD , ∴∠BEP=90°,∴EF= ![]() PG ,
PG ,
∵PF= ![]() PG(中点定义),∴EF=PF , ∴∠FEP=∠EPF , ∵∠BEP=∠EPC=90°,∴∠BEP-∠FEP=∠EPC-∠EPF , 即∠BEF=∠FPC , ∵四边形ABCD为菱形,∴AB=BC , ∠ABC=180°-∠A=70°,∵E , F分别为AB , BC的中点,∴BE=BF , ∠BEF=∠BFE=
PG(中点定义),∴EF=PF , ∴∠FEP=∠EPF , ∵∠BEP=∠EPC=90°,∴∠BEP-∠FEP=∠EPC-∠EPF , 即∠BEF=∠FPC , ∵四边形ABCD为菱形,∴AB=BC , ∠ABC=180°-∠A=70°,∵E , F分别为AB , BC的中点,∴BE=BF , ∠BEF=∠BFE= ![]() (180°-70°)=55°,∴∠FPC=55°.
(180°-70°)=55°,∴∠FPC=55°.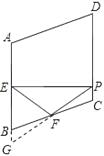
【解析】延长PF交AB的延长线于点G . 根据已知可得∠ABC , ∠BEF , ∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而不难求得∠FPC的度数.
【考点精析】关于本题考查的勾股定理的概念和菱形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
A.3×106
B.3×105
C.0.3×106
D.30×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ABC是平角,过点B任意作一条射线BD,将∠ABC分成∠DBA与∠DBC两个角.
(1)当∠DBA是什么角时,∠DBA>∠DBC?
(2)当∠DBA是什么角时,∠DBA=∠DBC?
(3)当∠DBA是什么角时,∠DBA<∠DBC?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界文化遗产长城总长约为6700000m,若将6700000用科学记数法表示为6.7×10n(n是正整数),则n的值为( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学生为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.
请根据以上信息,解答下列问题:
(1)将统计图补充完整;
(2)若该校共有1800名学生,根据以上调查结果估计该校全体学生每天完成作业所用总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位面向内部职工招聘高级管理人员一名.经初选、复选后,共有甲、乙、丙三名候选人进入最后的决赛.现对甲、乙、丙三人进行了笔试和面试两项测试,三人的测试成绩如下表所示: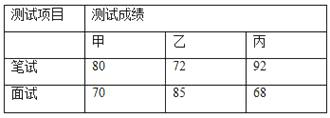
除了笔试、面试外,根据录用程序,该单位还组织了200名职工利用投票推荐的方式对三人进行民主评议,三人的得票率如下图所示(没有弃权票,每位职工只能推荐1人),每得一票记1分.
(1)甲的民主评议得分为多少?
(2)若根据笔试成绩、面试成绩、民主评议得分三项的平均成绩确定个人成绩,那么谁将被录用?
(3)根据实际需要,该单位将笔试、面试、民主评议三项得分按5:3:2的比例确定个人成绩,那么谁将被录用?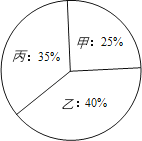
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班去体育用品商店购买羽毛球和羽毛球拍,每只羽毛球2元,每副羽毛球拍25元.甲商店说:“羽毛球拍和羽毛球都打9折优惠”,乙商店说:“买一副羽毛球拍赠2只羽毛球”.
(1)该班如果买2副羽毛球拍和20只羽毛球,问在甲、乙两家商店各需花多少钱?
(2)该班如果准备花90元钱全部用于买2副羽毛球拍和若干只羽毛球,请问到哪家商店购买更合算?
(3)该班如果必须买2副羽毛球拍,问当买多少只羽毛球时到两家商店购买同样合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com