
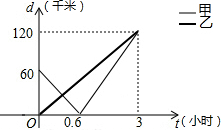
 甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )
甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据速度=路程÷时间,计算即可;
②根据图形可得甲船航行0.6小时到达B处,依此即可求解;
③根据图形可得甲、乙两船航行多少小时相遇,依此即可求解;
④分两种情形利用待定系数法求出分段函数的解析式,再列出不等式,解不等式即可.
解答 解:①乙的速度=120÷3=40(米/分),故正确;
②由图形可得甲船航行0.6小时到达B处,故错误;
③由图形可得甲、乙两船航行3小时相遇,故错误;
④设函数解析式为d1=kt+b,
0≤t≤0.6时,把(0,60)和(0.6,0)代入得d1=-100t+60,
0.6<t≤3时,把(0.6,0)和(3,120)代入得d1=50t-30;
d2=40t,
当0≤t<0.6时,d2+d1≥10,
即-100t+60+40t≥10,解得t≤$\frac{5}{6}$,
∵0≤t<0.6,
∴当0≤t<0.6时,甲、乙两船的距离不小于10千米;
当0.6≤t≤3时,d2-d1≥10,即40t-(50t-30)≥10,解得t≤2,
∵0.6≤t≤3,
∴当0.6≤t≤2时,甲、乙两船的距离不小于10千米.
综上所述,甲、乙两船的距离不小于10千米的时间段是0≤t≤2,故错误.
故选:A.
点评 本题考查一次函数的应用、一元一次不等式等知识,解题的关键是利用待定系数法确定函数解析式,学会利用不等式解决实际问题,属于中考常考题型.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{8}$=4 | C. | $\sqrt{6}$÷$\sqrt{5}$=$\frac{\sqrt{6}}{5}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
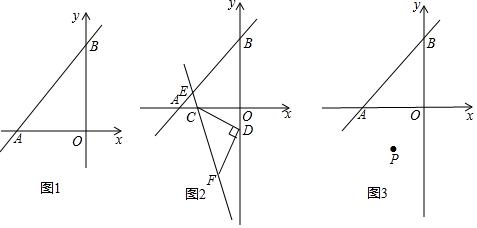
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
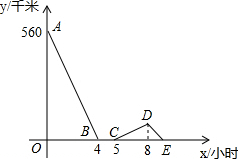 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
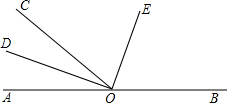 如图,点O为直线AB上的一点,∠BOC=130°,OE平分∠BOC,DO⊥OE.
如图,点O为直线AB上的一点,∠BOC=130°,OE平分∠BOC,DO⊥OE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com