
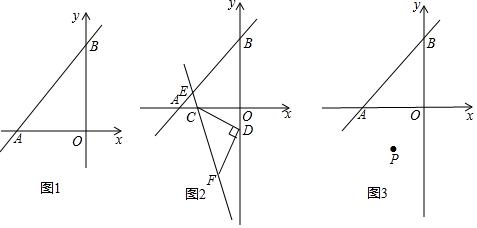
分析 (1)由直线解析式可分别用m表示出A、B的坐标,利用△AOB的面积可得到关于m的方程,则可求得m的值;
(2)过F作FG⊥y轴于点G,可证得△CDF为等腰直角三角形,则可证得△CDO≌△DFG,则可求得FG和OG的长,可求得F点坐标;
(3)可分别求得点P落在AO边上和落在AB边上时的对应的时间,则可求得P在△ABO内部时t的取值范围.
解答 解:
(1)由题意可知A、B坐标分别为(-m,0)、(0,-m),
∴${S_{△AOB}}=\frac{1}{2}AO•BO=\frac{1}{2}{m^2}=8$,解得m=±4,
又∵B点在y轴正半轴,即m>0,
∴m=4;
(2)如图,作FG⊥y轴于G,由题意可知OC=3,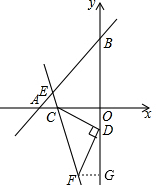
设∠AEC=∠CDO=x°,
则∠FCO=∠ACE=135°-x°,∠OCD=90°-x°,∠DCF=135°-x°-(90°-x°)=45°,
∴△CDF为等腰直角三角形,
∴CD=DF,
∵∠OCD+∠ODC=∠ODC+∠FDG=90°,
∴∠OCD=∠FDG,
在△CDO和△DFG中
$\left\{\begin{array}{l}{∠OCD=∠FDG}\\{∠COD=∠FGD}\\{CD=FD}\end{array}\right.$
∴△CDO≌△DFG(AAS),
∴OD=FG=2,DG=CO=3,
∴OG=OD+DG=5,
∴F(-2,-5);
(3)当P点落在AO边上时,由题意得0-2t=-2,解得t=1;
当P点落在AB边上时,由题意得(-1-t)+m-2t=-2,由(1)可知,m=4,解得$t=\frac{5}{3}$;
∴若点P落在△ABO内部(不包含三角形的边),则t的取值范围为$1<t<\frac{5}{3}$.
点评 本题为一次函数的综合应用,涉及三角形的面积、全等三角形的判定和性质、等腰直角三角形的判定等知识.在(1)中用m表示出△AOB的面积是解题的关键,在(2)中构造三角形全等求得OG和FG的长是解题的关键,在(3)中确定出P点的极端位置时的t的值是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
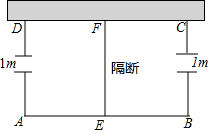 如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.
如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
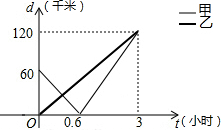 甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )
甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
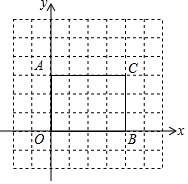 如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).
如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
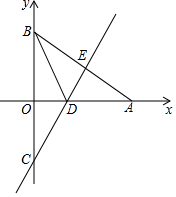 如图,A,B分别在x轴与y轴上,AB=12,∠OAB=30°,将△OAB沿直线ED对折,使点A与点B重合,直线ED分别交y轴、x轴和AB于点C、点D和点E.
如图,A,B分别在x轴与y轴上,AB=12,∠OAB=30°,将△OAB沿直线ED对折,使点A与点B重合,直线ED分别交y轴、x轴和AB于点C、点D和点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com