
| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |
分析 设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为$\frac{15-2x}{3}$个,分两种情况讨论:①当0≤x<3时;②当3≤x时,利用一次函数的性质即可解答.
解答 解:设购买A种型号盒子x个,购买盒子所需要费用为y元,
则购买B种盒子的个数为$\frac{15-2x}{3}$个,
①当0≤x<3时,y=5x+$\frac{15-2x}{3}×6$=x+30,
∵k=1>0,
∴y随x的增大而增大,
∴当x=0时,y有最小值,最小值为30元;
②当3≤x时,y=5x+$\frac{15-2x}{3}×6$-4=26+x,
∵k=1>0,
∴y随x的增大而增大,
∴当x=3时,y有最小值,最小值为29元;
综合①②可得,购买盒子所需要最少费用为29元.
故答案为:29.
点评 本题考查了一次函数的应用,解决本题的关键是根据题意列出函数解析式,利用一次函数的性质解决最小值的问题,注意分类讨论思想的应用.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
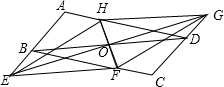 如图,过平行四边形ABCD的对角线BD的中点O作两条互相垂直的直线,且交AB、CD的延长线于点E,G,交BC,AD于点F,H,连接EF,FG,GH,EH.
如图,过平行四边形ABCD的对角线BD的中点O作两条互相垂直的直线,且交AB、CD的延长线于点E,G,交BC,AD于点F,H,连接EF,FG,GH,EH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
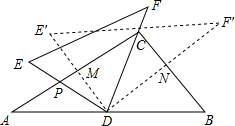 将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转α(0°<α<60°),DE′交AC于点M,DF′交BC于点N,则$\frac{PM}{CN}$的值为( )
将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转α(0°<α<60°),DE′交AC于点M,DF′交BC于点N,则$\frac{PM}{CN}$的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
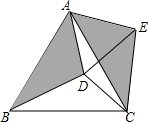 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
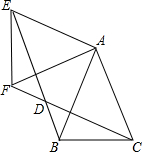 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
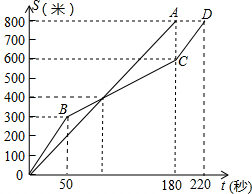 在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )| A. | 甲的速度随时间的增加而增大 | B. | 乙的平均速度比甲的平均速度大 | ||
| C. | 在起跑后第180秒时,两人相遇 | D. | 在起跑后第50秒时,乙在甲的前面 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
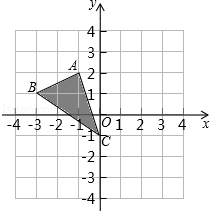 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com