
| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
|
|
| 1 |
| 20 |
| 1 |
| 4 |
| b |
| 2a |
| 1 |
| 2 |


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
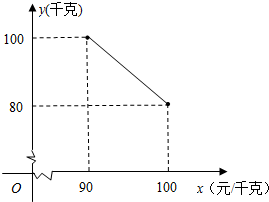 某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.查看答案和解析>>
科目:初中数学 来源: 题型:
| x | 25 | 28 | 30 | 32 | 35 |
| y | 250 | 220 | 200 | 180 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:
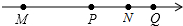 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )| A、点M | B、点N | C、点P | D、点Q |
查看答案和解析>>
科目:初中数学 来源: 题型:
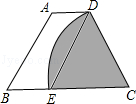 如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )
如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )| A、2π | B、4π | C、6π | D、12π |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
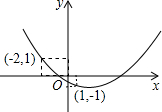 如图,二次函数y=ax2+bx+c的图象经过点(1,-1)和(-2,1),下列关于此二次函数的叙述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,-1)和(-2,1),下列关于此二次函数的叙述,正确的是( )| A、当x=0时,y的值小于-1 |
| B、当x=-3时,y的值大于1 |
| C、当x=5时,y的值等于0 |
| D、当x=1时,y的值大于1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com