
 已知,如图在平面直角坐标系中,S△ABO=6,OA=OB,BC=12,求△ABC三个顶点的坐标.
已知,如图在平面直角坐标系中,S△ABO=6,OA=OB,BC=12,求△ABC三个顶点的坐标. 分析 先根据三角形面积求出OA的长,再根据OA=OB可得OB,最后由BC=10可得OC,继而可得答案.
解答 解:∵S△ABO=$\frac{1}{2}$OB•OA=6,OA=OB,
∴OA=OB=2$\sqrt{3}$,
∴A(0,2$\sqrt{3}$)、B(-2$\sqrt{3}$,0).
∵BC=12,
∴OC=BC-OB=12-2$\sqrt{3}$,
∴C(12-2$\sqrt{3}$,0).
综上所述,A(0,2$\sqrt{3}$)、B(-2$\sqrt{3}$,0)、C(12-2$\sqrt{3}$,0).
点评 此题考查的知识点是三角形的面积、等腰直角三角形,关键是写三角形顶点的坐标时,要特别注意根据点所在的位置来确定坐标正负情况.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 试验次数 | 10 | 50 | 100 | 200 | 500 | 1000 | 2000 |
| 事件发生的 频率 | 0.245 | 0.248 | 0.251 | 0.253 | 0.249 | 0.252 | 0.251 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨 | |
| B. | 随机抛掷一枚质地均匀的硬币,落地后一定反面向上 | |
| C. | 在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖 | |
| D. | 同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
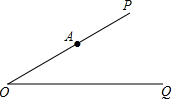 如图,∠POQ=30°,点A在OP边上,且OA=6,试在OQ边上确定一点B,使得△AOB是等腰三角形,则满足条件的点B个数为( )
如图,∠POQ=30°,点A在OP边上,且OA=6,试在OQ边上确定一点B,使得△AOB是等腰三角形,则满足条件的点B个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com