
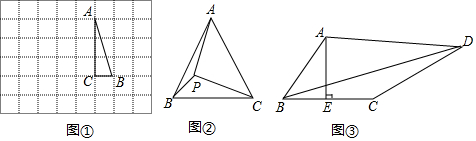
分析 【操作发现】(1)根据旋转角,旋转方向画出图形即可;
(2)只要证明△ABB′是等腰直角三角形即可;
【问题解决】如图②,将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,只要证明∠PP′C=90°,利用勾股定理即可解决问题;
【灵活运用】如图③中,由AE⊥BC,BE=EC,推出AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,只要证明∠GDC=90°,可得CG=$\sqrt{D{G}^{2}+C{D}^{2}}$,由此即可解决问题;
解答 解:【操作发现】(1)如图所示,△AB′C′即为所求;
(2)连接BB′,将△ABC绕点A按顺时针方向旋转90°,
∴AB=AB′,∠B′AB=90°,
∴∠AB′B=45°,
故答案为:45°;
【问题解决】如图②,
∵将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,
∴△APP′是等边三角形,∠AP′C=∠APB=360°-90°-120°=150°,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=90°,∠P′PC=30°,
∴PP′=$\frac{\sqrt{3}}{2}$PC,即AP=$\frac{\sqrt{3}}{2}$PC,
∵∠APC=90°,
∴AP2+PC2=AC2,即($\frac{\sqrt{3}}{2}$PC)2+PC2=72,
∴PC=2$\sqrt{7}$,
∴AP=$\sqrt{21}$,
∴S△APC=$\frac{1}{2}$AP•PC=7$\sqrt{3}$;
【灵活运用】如图③中,∵AE⊥BC,BE=EC,
∴AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,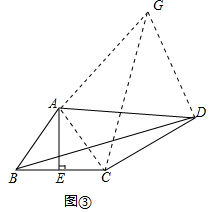
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=kAB,
∴DG=kBC=4k,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=$\sqrt{D{G}^{2}+C{D}^{2}}$=$\sqrt{16{k}^{2}+25}$.
∴BD=CG=$\sqrt{16{k}^{2}+25}$.
点评 本题考查相似形综合题、等边三角形的判定和性质、等腰三角形的判定和性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会用旋转法添加辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
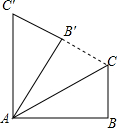 如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.
如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
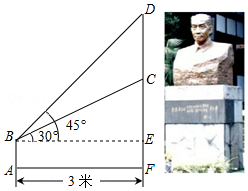 如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7)
如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y=mx(m为常数,且m≠0)与双曲线y=$\frac{k}{x}$(k为常数,且k≠0)相交于A(-2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为12.
如图,直线y=mx(m为常数,且m≠0)与双曲线y=$\frac{k}{x}$(k为常数,且k≠0)相交于A(-2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
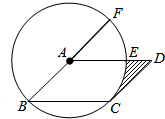 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,曲线l是由函数y=$\frac{6}{x}$在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(-4$\sqrt{2}$,4$\sqrt{2}}$),B(2$\sqrt{2}$,2$\sqrt{2}}$)的直线与曲线l相交于点M、N,则△OMN的面积为8.
如图,曲线l是由函数y=$\frac{6}{x}$在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(-4$\sqrt{2}$,4$\sqrt{2}}$),B(2$\sqrt{2}$,2$\sqrt{2}}$)的直线与曲线l相交于点M、N,则△OMN的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
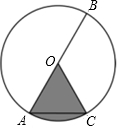 如图,AB是⊙O的直径,AC是弦,AC=3,∠BOC=2∠AOC.若用扇形OAC(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是$\frac{1}{2}$.
如图,AB是⊙O的直径,AC是弦,AC=3,∠BOC=2∠AOC.若用扇形OAC(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com