
 如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7)
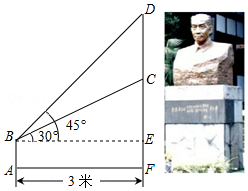
如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7) 分析 由BE=3、∠CBE=30°可知CE=BEtan∠CBE=$\sqrt{3}$,由∠DBE=45°知DE=BE=3,根据CD=DE-CE可得答案.
解答 解:由已知得∠CBE=30°,∠BED=90°,∠DBE=45°,
在Rt△BCE中,BE=3,∠CBE=30°,
∴CE=BEtan∠CBE=3×tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
在Rt△BED中,∵∠DBE=45°,
∴DE=BE=3,
则CD=DE-CE=3-$\sqrt{3}$≈1.3m.
答:塑像CD高约1.3m.
点评 本题考查了解直角三角形的应用-仰角俯角问题,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
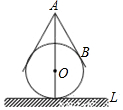 用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为$\frac{720π}{13}$cm2.
用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为$\frac{720π}{13}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com