练习册

  • 练习册
  • 试题
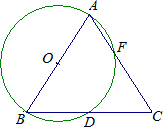    精英家教网 > 初中数学 > 题目详情
    21、一边是3，一边是5的等腰三角形周长是
    11或13
    ．
    分析：题目给出等腰三角形有两条边长为3和5，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
    解答：解：当3为等腰三角形的腰长时，
    3+3=6＞5，符合两边之和大于第三边，
    三角形周长为3+3+5=11；
    当5为等腰三角形的腰长时，
    5+5=10＞3，符合两边之和大于第三边，
    三角形周长为5+5+3=13．
    故填11或13．
    点评：本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC交⊙O于点F．
    （1）AB与AC的大小有什么关系？为什么？
    （2）按角的大小分类，请你判断△ABC属于哪一类三角形，并说明理由．

    小明按下面的方法作出了∠MON的平分线：
    ①反向延长射线OM；
    ②以点O为圆心，任意长为半径作圆，分别交∠MON的两边于点A、B，交射线OM的反向延长精英家教网线于点C；
    ③连接CB；
    ④以O为顶点，OA为一边作∠AOP=∠OCB．
    （1）根据上述作图，射线OP是∠MON的平分线吗？并说明理由．
    （2）若过点A作⊙O的切线交射线OP于点F，连接AB交OP于点E，当∠MON=60°、OF=10时，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年山东省泰安市九年级上学期期末考试数学试卷（解析版） 题型：解答题

    在某市开展的环境创优活动中，某居民小区要在一块靠墙（墙长15米）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成，若设花园与墙平行的一边长为x(m)，花园的面积为y(m2)。

    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；

    （2）满足条件的花园面积能达到200m2吗？若能，求出此时x的值，若不能，说明理由：

    （3）根据(1)中求得的函数关系式，判断当x取何值时，花园的面积最大？最大面积是多少？

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    能使方程左右两边相等的未知数的①______，叫做方程的解．
    求方程的解的②______叫做解方程．求方程的解就是将方程变形为③______的形式．
    等式的两条性质是④______的依据．
    （1）等式两边都加上或减去同一个数或同一个整式，所得结果仍是⑤______．
    （2）等式两边都乘或除以同一个⑥______的数，所得结果仍是等式．
    方程中的某些项⑦______后，从方程的一边移到另一边，这样的变形叫做⑧______．
    一般地，解一元一次方程的一般步骤：去分母、⑨______、移项、⑩______、未知数的?______化为1．以上步骤不是一成不变的，在解方程时要根据方程的特点灵活运用这些步骤．
    去分母和去括号时注意不能漏乘；分数线既具有除号的作用，又具有括号的作用，当分子是多项式时，去分母后，原先的括号要补上；另外，移项时特别注意要改变符号．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    能使方程左右两边相等的未知数的①______，叫做方程的解．
    求方程的解的②______叫做解方程．求方程的解就是将方程变形为③______的形式．
    等式的两条性质是④______的依据．
    （1）等式两边都加上或减去同一个数或同一个整式，所得结果仍是⑤______．
    （2）等式两边都乘或除以同一个⑥______的数，所得结果仍是等式．
    方程中的某些项⑦______后，从方程的一边移到另一边，这样的变形叫做⑧______．
    一般地，解一元一次方程的一般步骤：去分母、⑨______、移项、⑩______、未知数的?______化为1．以上步骤不是一成不变的，在解方程时要根据方程的特点灵活运用这些步骤．
    去分母和去括号时注意不能漏乘；分数线既具有除号的作用，又具有括号的作用，当分子是多项式时，去分母后，原先的括号要补上；另外，移项时特别注意要改变符号．

    查看答案和解析>>

    科目：初中数学 来源：第3章《圆的基本性质》中考题集（22）：3.4 圆周角（解析版） 题型：解答题

    如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC交⊙O于点F．
    （1）AB与AC的大小有什么关系？为什么？
    （2）按角的大小分类，请你判断△ABC属于哪一类三角形，并说明理由．

    小明按下面的方法作出了∠MON的平分线：
    ①反向延长射线OM；
    ②以点O为圆心，任意长为半径作圆，分别交∠MON的两边于点A、B，交射线OM的反向延长线于点C；
    ③连接CB；
    ④以O为顶点，OA为一边作∠AOP=∠OCB．
    （1）根据上述作图，射线OP是∠MON的平分线吗？并说明理由．
    （2）若过点A作⊙O的切线交射线OP于点F，连接AB交OP于点E，当∠MON=60°、OF=10时，求AE的长．

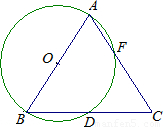
    查看答案和解析>>

    同步练习册答案