
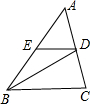 如图,BD平分∠ABC,ED∥BC.∠ABD=36°.求∠EDB、∠AED的度数.
如图,BD平分∠ABC,ED∥BC.∠ABD=36°.求∠EDB、∠AED的度数. ∠ABC(平分线的性质),
∠ABC(平分线的性质), ∠ABC,又由ED∥BC,根据两直线平行,内错角相等及同位角相等,可得∠EDB=∠DBC=36°,∠AED=∠ABC=72°.
∠ABC,又由ED∥BC,根据两直线平行,内错角相等及同位角相等,可得∠EDB=∠DBC=36°,∠AED=∠ABC=72°.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com