
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90度.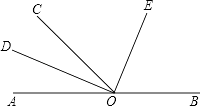
(1)请你数一数,图中有多少个角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
【答案】
(1)解:图中有9个小于平角的角
(2)解:因为OD平分∠AOC,∠AOC=50°
所以∠AOD= ![]() =25°,所以∠BOD=180°﹣25°=155°
=25°,所以∠BOD=180°﹣25°=155°
(3)解:因为∠BOE=180°﹣∠DOE﹣∠AOD=180°﹣90°﹣25°=65°
∠COE=90°﹣25°=65°
所以∠BOE=∠COE.即OE平分∠BOC
【解析】(1)按照顺序数,以OA为边顺时针数有3个角,以OD为边的有3个角,以OC为边的有2个角,以OE为边的有1个角,一共由9个角。
(2)观察图形及已知条件∠BOD=180°-∠AOD,只需求出∠AOD的度数,根据角平分线的定义易求出。
(3)根据题意分别求出∠BOE和∠COE的度数即可判断。


科目:初中数学 来源: 题型:
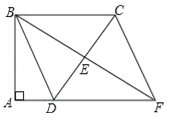
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据. 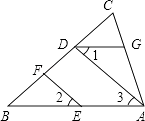
【解】∵EF∥AD(已知)
∴∠2=()
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥()
∴∠BAC+=180°()
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
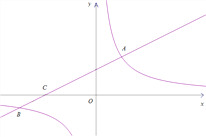
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线![]() 的解析式;
的解析式;
(2)若点P在x轴上,且![]() ,求点P的坐 标(直接写出结果).
,求点P的坐 标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
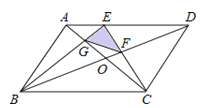
【题目】如图,平行四边形ABCD中,E是AD上的一点,且AE=![]() AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
A. ![]() S B.
S B. ![]() S C.
S C. ![]() S D.
S D. ![]() S
S
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械厂加工车间有84名工人,平均每人每天加工大齿轮16个或者小齿轮10个,已知1个大齿轮与2个小齿轮刚好配成一套,问分别安排多少名工人加工大,小齿轮,才能使每天加工的大小齿轮刚好配套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com