
在分别标有2,4,6,7,8,11,12和13的8张卡片中任取2张,把抽出的2张上的数字组成一个分数.
①估计能构成既约分数的机会有多大?
②构成可约分数的机会有多大?
③这两个机会和是多少?
|
任取2张卡片,所有可能出现的结果为: (2,4),(2,6),(2,7),(2,8),(2,11),(2,12),(2,13),(4,6),(4,7),(4,8),(4,11),(4,12),(4,13),(6,7),(6,8),(6,11),(6,12),(6,13),(7,8),(7,11),(7,12),(7,13),(8,11),(8,12),(8,13),(11,12),(11,13),(12,13)共28种情况. ①构成既约分数的有:(2,7),(2,11),(2,13),(4,7),(4,11),(4,13),(6,7),(6,11),(6,13),(7,8),(7,11),(7,12),(7,13),(8,11),(8,13),(11,12),(11,13),(12,13),共18种情况, 所以估计出现既约分数的机会为
②构成可约分数的有(2,4),(2,6),(2,8),(2,12),(4,6),(4,8),(4,12),(6,8),(6,12),(8,12),共10种情况,所以构成可约分数的机会为
③这两个机会和为1. |
|
要估计某一事件发生的可能性的大小,关键是寻求机会值,而寻求机会值时必须搞清该随机事件发生的情况有几种,以及可能发生的事件共有几种. |


科目:初中数学 来源: 题型:
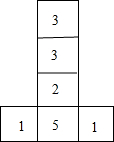 六个面上分别标有1,1,2,3,3,5六个数字的均匀六方体表面如图所示,掷这个六方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该六方体,就能得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线l,且这条直线l经过点(4,7).那么,他第三次掷得的点也在这条直线上的概率是
六个面上分别标有1,1,2,3,3,5六个数字的均匀六方体表面如图所示,掷这个六方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该六方体,就能得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线l,且这条直线l经过点(4,7).那么,他第三次掷得的点也在这条直线上的概率是查看答案和解析>>
科目:初中数学 来源: 题型:
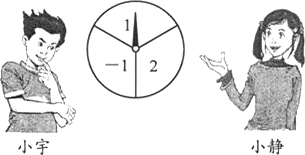
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:新课标3维同步训练与评价 数学(北师大版·七年级下册) 题型:044
在分别标有1,2,3,4的四张卡片中任取两张,排成一个两位数,指出这个两位数为奇数的可能性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com