
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是 . 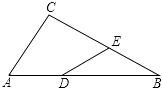
【答案】2≤AD<3
【解析】解:以D为圆心,AD的长为半径画圆
①如图1,当圆与BC相切时,DE⊥BC时,
∵∠ABC=30°,
∴DE= ![]() BD,
BD,
∵AB=6,
∴AD=2;
②如图2,当圆与BC相交时,若交点为B或C,则AD= ![]() AB=3,
AB=3,
∴AD的取值范围是2≤AD<3.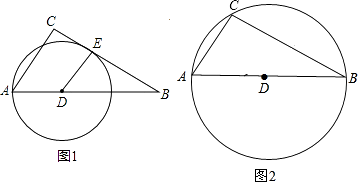
【考点精析】本题主要考查了含30度角的直角三角形和直线与圆的三种位置关系的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数y=﹣ ![]() 的图像和一次函数y=kx﹣1的图像都经过点P(m,﹣3m).
的图像和一次函数y=kx﹣1的图像都经过点P(m,﹣3m). 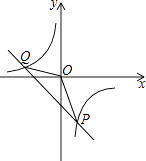
(1)求点P的坐标和这个一次函数的表达式;
(2)若这两个图像的另一个交点Q纵坐标为2,O为坐标原点,求△POQ的面积;
(3)若点M(a,y1)和点N(a+1,y2)都在这个反比例函数的图像上,比较y1和y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,抛物线![]() 经过
经过
A(-1,0)、B(0,3)两点,与![]() 轴交于另一点C,顶点为D.
轴交于另一点C,顶点为D.
(1)求该抛物线的解析式及点C、D的坐标;
(2)经过点B、D两点的直线与![]() 轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
(3)如图(2)P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ的最大面积和此时Q点的坐标.
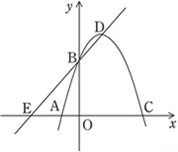
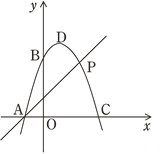
图(1) 图(2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.![]()
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若C为直线AB上线段AB之外的任一点,且AC=m,CB=n,则线段MN的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.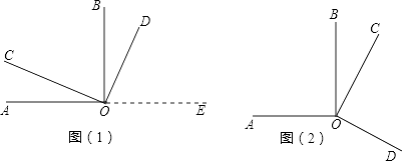
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
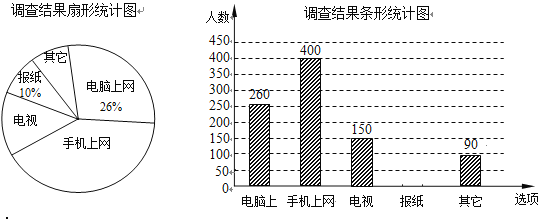
根据以上信息解答下列问题:
(1)这次抽样调查的样本容量是 ;
(2)通过“电视”了解新闻的人数占被调查人数的百分比为 ;扇形统计图中, “手机上网”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有70万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com