
 x+4分别交x轴、y轴于A、B两点.
x+4分别交x轴、y轴于A、B两点.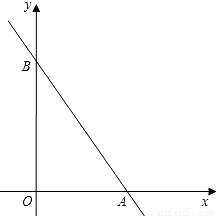
 x+4分别交x轴、y轴于A、B两点,所以分别令x=0、y=0,即可求出A、B的坐标;
x+4分别交x轴、y轴于A、B两点,所以分别令x=0、y=0,即可求出A、B的坐标;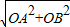 =5,所以sin∠OBA=
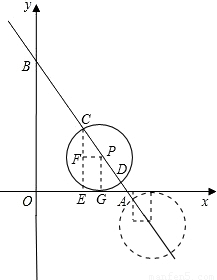
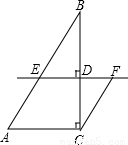
=5,所以sin∠OBA= ,要求点C的横坐标,可过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,则∠FCP=∠OBA,PF=m-n.
,要求点C的横坐标,可过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,则∠FCP=∠OBA,PF=m-n. x+4上,所以PC=PG=-
x+4上,所以PC=PG=- m+4,利用三角函数可得PF=PC•sin∠FCP=PC•sin∠OBA,即可得到关于m、m的关系式,整理即可;
m+4,利用三角函数可得PF=PC•sin∠FCP=PC•sin∠OBA,即可得到关于m、m的关系式,整理即可;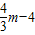 ,PF=PC•sin∠FCP=PC•sin∠OBA,整理即可得到另一个m、n的关系式;
,PF=PC•sin∠FCP=PC•sin∠OBA,整理即可得到另一个m、n的关系式; m-
m-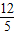 ,因为△BOC为等腰三角形,所以需要分情况讨论:
,因为△BOC为等腰三角形,所以需要分情况讨论: ,即n=
,即n= ,即
,即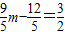 ,解之即可;
,解之即可; ,又因OE+AE=OA,就可得到关于m的方程,解之即可;
,又因OE+AE=OA,就可得到关于m的方程,解之即可; x+4=0,x=3.
x+4=0,x=3.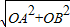 =5,
=5, .
.
 m+4,
m+4, m+4)×
m+4)× .
. m-
m-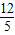 .(5分)
.(5分)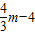 ,PF=PC•sin∠FCP=PC•sin∠OBA,
,PF=PC•sin∠FCP=PC•sin∠OBA, m-4)×
m-4)× .
. m+
m+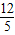 .(7分)
.(7分) m-
m-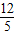 ,
, .
.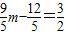 ,解得m=
,解得m=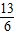 .(9分)
.(9分) .
.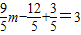 ,解得m=
,解得m= .
.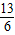 或m=
或m= 时,△BOC为等腰三角形.(11分)
时,△BOC为等腰三角形.(11分)

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
| n | 1 | 2 | 3 | … |
| Sn | … |

查看答案和解析>>
科目:初中数学 来源:2006年河南省中考数学试卷(大纲卷)(解析版) 题型:解答题
| n | 1 | 2 | 3 | … |
| Sn | … |

查看答案和解析>>
科目:初中数学 来源:2006年河南省中考数学试卷(课标卷)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年河南省中考数学试卷(大纲卷)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com