
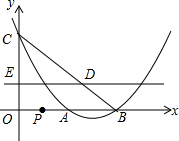
 抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x+2与x轴交于A,B两点(OA<OB),与y轴交于点C.
抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x+2与x轴交于A,B两点(OA<OB),与y轴交于点C.分析 (1)在抛物线的解析式中,令y=0,令x=0,解方程即可得到结果;
(2)①由题意得:OP=2t,OE=t,通过△CDE∽△CBO得到$\frac{CE}{CO}=\frac{ED}{OB}$,即$\frac{2-t}{2}=\frac{DE}{4}$,求得$\frac{1}{OP}+\frac{1}{ED}$有最小值1,即可求得结果;
②存在,求得抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x+2的对称方程为x=3,设F(3,m),当△EFP为直角三角形时,①当∠EPF=90°时,②当∠EFP=90°时,③当∠PEF=90°时,根据勾股定理列方程即可求得结果.
解答 解:(1)在抛物线的解析式中,令y=0,即$\frac{1}{4}$x2-$\frac{3}{2}$x+2=0,
解得:x1=2,x2=4,∵OA<OB,
∴A(2,0),B(4,0),
在抛物线的解析式中,令x=0,得y=2,
∴C(0,2),
(2)①由题意得:OP=2t,OE=t,
∵DE∥OB,
∴△CDE∽△CBO,
∴$\frac{CE}{CO}=\frac{ED}{OB}$,即$\frac{2-t}{2}=\frac{DE}{4}$,
∴DE=4-2t,
∴$\frac{1}{OP}+\frac{1}{ED}=\frac{1}{2t}+\frac{1}{4-2t}=\frac{1}{{-t}^{2}+2t}=\frac{1}{1{-(t-1)}^{2}}$,
∵0<t<2,1-(t-1)2始终为正数,且t=1时,1-(t-1)2有最大值1,
∴t=1时,$\frac{1}{1-(t-1)^{2}}$有最小值1,
即t=1时,$\frac{1}{OP}+\frac{1}{ED}$有最小值1,此时OP=2,OE=1,
∴E(0,1),P(2,0);
②存在,
∵抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x+2的对称轴方程为x=3,
设F(3,m),
∴EP2=5,PF2=(3-2)2+m2,EF2=(m-1)2+32,
当△EFP为直角三角形时,
①当∠EPF=90°时,
EP2+PF2=EF2,
即5+1+m2=(m-1)2+32,
解得:m=2,
②当∠EFP=90°时,
EF2+FP2=PE2,
即(m-1)2+32+(3-2)2+m2=5,
此方程无解,不合题意舍去,
∴当∠EFP=90°时,
这种情况不存在,
③当∠PEF=90°时,
EF2+PE2=PF2,
即(m-1)2+32+5=(3-2)2+m2,
解得:m=7,
∴F(3,2),(3,7).
点评 本题考查了根据函数的解析式求点的坐标,相似三角形的判定和性质,求代数式的最值,勾股定理,存在性问题,在求有关存在性问题时要注意分析题意分情况讨论结果.


科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{2(x-1)≤-1①}\\{2x+3>1②}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2(x-1)≤-1①}\\{2x+3>1②}\end{array}\right.$,并把它的解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.
如图,?ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com