
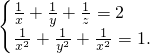 ,则
,则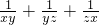 的值是
的值是


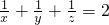 通分变为
通分变为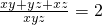 ,接着得到xy+yz+zx=2xyz,然后两边同时平方得到x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,然后把
,接着得到xy+yz+zx=2xyz,然后两边同时平方得到x2y2+y2z2+z2x2+2xyz(x+y+z)=4x2y2z2①,然后把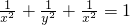 通分变为
通分变为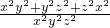 =1,然后变为x2y2+y2z2+z2x2=x2y2z2,接着把它代入①中即可解决问题.
=1,然后变为x2y2+y2z2+z2x2=x2y2z2,接着把它代入①中即可解决问题.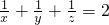 ,
,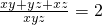 ,
,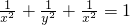 ,
,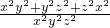 =1,
=1,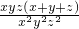 =
= ,
,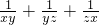 =
= .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
1.红用下面的方法对![]() 进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
| 方程 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 关于x的方程
( 且 |
|
|
|
2.设![]() 是一元二次方程
是一元二次方程![]()
![]() 的两个实根,根据观察表格中的规律,写出二次三项式
的两个实根,根据观察表格中的规律,写出二次三项式![]()
![]() 的因式分解与
的因式分解与![]() 之间的关系式。
之间的关系式。
查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 +k)k,k为实数.
+k)k,k为实数. 是否为一定值?若是,请求出该定值;若不是,请说明理由;
是否为一定值?若是,请求出该定值;若不是,请说明理由;查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省惠州市惠城区七校九年级上学期联考数学卷 题型:解答题
1.红用下面的方法对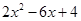 进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
进行因式分解,请你仿照他的方法分解下面另外三个二次三项式,并把你的解答过程填写在下面的表格中.
|
方程 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
关于x的方程
( 且 |
|
|
|
2.设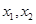 是一元二次方程
是一元二次方程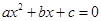
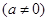 的两个实根,根据观察表格中的规律,写出二次三项式
的两个实根,根据观察表格中的规律,写出二次三项式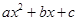
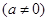 的因式分解与
的因式分解与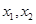 之间的关系式。
之间的关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com