
解决下面的数学问题
如图:已知∠AOB=80°,射线OC在∠AOB内的内部,OD、OE分别平分∠AOC、∠COB,求∠DOE的度数。

(2)如图:如果将(1)中射线OC顺时针旋转到∠AOB的外部,其他条件不变。你还能求出∠DOE的度数吗?
(1)40°;(2)40°
【解析】
试题分析:(1)根据角平分线的性质可得∠DOC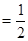 ∠AOC,∠COE
∠AOC,∠COE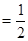 ∠BOC,则∠DOE=∠DOC+∠COE
∠BOC,则∠DOE=∠DOC+∠COE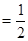 ∠AOC
∠AOC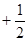 ∠BOC
∠BOC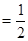 ∠AOB,即可求得结果;
∠AOB,即可求得结果;
(2)根据角平分线的性质可得∠DOC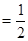 ∠AOC,∠COE
∠AOC,∠COE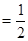 ∠BOC,则∠DOE=∠DOC-∠COE
∠BOC,则∠DOE=∠DOC-∠COE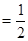 ∠AOC
∠AOC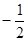 ∠BOC
∠BOC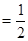 ∠AOB,即可求得结果.
∠AOB,即可求得结果.
(1)∵OD、OE分别平分∠AOC、∠COB
∴∠DOC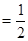 ∠AOC,∠COE
∠AOC,∠COE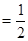 ∠BOC
∠BOC
∴∠DOE=∠DOC+∠COE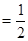 ∠AOC
∠AOC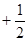 ∠BOC
∠BOC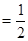 ∠AOB
∠AOB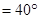 ;
;
(2)∵OD、OE分别平分∠AOC、∠COB
∴∠DOC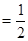 ∠AOC,∠COE
∠AOC,∠COE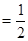 ∠BOC
∠BOC
∴∠DOE=∠DOC-∠COE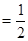 ∠AOC
∠AOC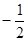 ∠BOC
∠BOC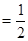 ∠AOB
∠AOB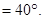
考点:比较角的大小,角平分线的性质
点评:解题的关键是熟练掌握角的平分线把角分成相等的两个小角,且都等于大角的一半,注意本题要有整体意识.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 3 |
| 4 |
| 5 |
| 13 |
| 9 |
| 17 |
| 14 |
| 23 |
| 19 |
| 28 |
| a |
| b |
| a+m |
| b+m |
| a |
| b |
| a+m |
| b+m |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏泰州民兴实验中学七年级上学期期末考试数学试卷(带解析) 题型:解答题
解决下面的数学问题
如图:已知∠AOB=80°,射线OC在∠AOB内的内部,OD、OE分别平分∠AOC、∠COB,求∠DOE的度数。
(2)如图:如果将(1)中射线OC顺时针旋转到∠AOB的外部,其他条件不变。你还能求出∠DOE的度数吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com