
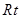 △
△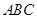 中,∠
中,∠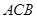 =90o,
=90o,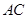 =
=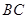 =1,将
=1,将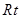 △
△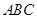 绕
绕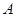 点逆时针旋转30o后得到
点逆时针旋转30o后得到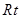 △
△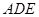 ,点
,点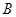 经过的路径为弧
经过的路径为弧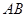 ,则图中阴影部分的面积是 。(结果用
,则图中阴影部分的面积是 。(结果用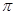 表示)
表示)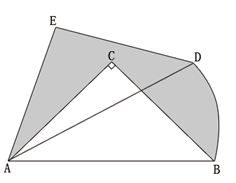
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源:不详 题型:解答题
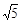 ,PB=
,PB=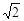 ,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.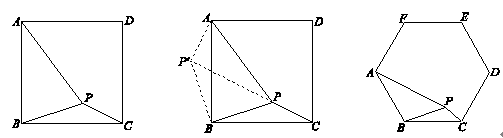
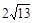 ,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
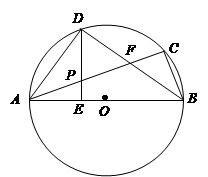
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.经过两点有且只有一条直线 | B.平行四边形的对角线相等 |
| C.两腰相等的梯形叫做等腰梯形 | D.圆的切线垂直于经过切点的半径 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com