
 如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )| A. | 4cm | B. | 5cm | C. | $\frac{15}{4}$cm | D. | $\frac{25}{4}$cm |
分析 由勾股定理求出AB,由折叠的性质得出∠DEB=90°,AE=BE=$\frac{1}{2}$AB=5,在Rt△BDE中,由三角函数即可求出DE的长.
解答 解:∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,tanB=$\frac{AC}{BC}$=$\frac{6}{8}$=$\frac{3}{4}$,
由折叠的性质得:∠DEB=90°,AE=BE=$\frac{1}{2}$AB=5,
∴tanB=$\frac{DE}{BE}$=$\frac{3}{4}$,
∴DE=$\frac{3}{4}$BE=$\frac{3}{4}$×5=$\frac{15}{4}$(cm).
故选:C.
点评 本题考查了翻折变换的性质、勾股定理、三角函数;熟练掌握翻折变换的性质,并能进行推理计算是解决问题的关键.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解飞行员视力的达标率应使用抽样调查 | |
| B. | 一组数据3,6,6,7,9的中位数是6 | |
| C. | 从2000名学生中选200名学生进行抽样调查,样本容量为2000 | |
| D. | 掷一枚质地均匀的硬币,正面朝上是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
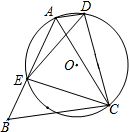 已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.
已知如图,△ACD内接于⊙O,E为⊙O上一点,且ED=EC,过点C作BC∥AD交AE的延长线于点B.若cosB=$\frac{3}{5}$,BC=2BE,AE=7,则ED=$\sqrt{65}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
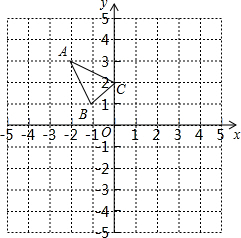 △ABC在平面直角坐标系xOy中的位置如所示.
△ABC在平面直角坐标系xOy中的位置如所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
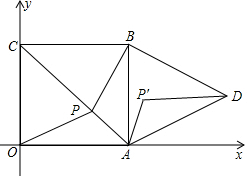 如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.
如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
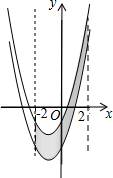 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )| A. |  | B. | 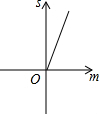 | C. | 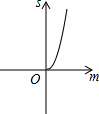 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
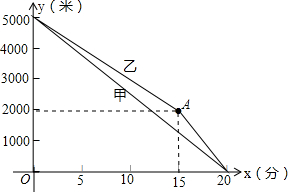 甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com