
(本题满分9分)如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点
D,DE⊥AC,交AC的延长线于点E.

(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AE=8,⊙O的半径为5,求DE的长.
(1)直线DE与⊙O相切,见解析;(2)4
【解析】
试题分析:(1)连接OD,由AD平分∠BAC ,EA∥OD证出OD⊥DE,即可得证直线DE与⊙O相切;
(2)作DF⊥AB,垂足为F,证明△EAD≌△FAD,得出OA=OD=5,OF=3,再由勾股定理得DF=4,进而求出DE=DF=4.
试题解析:(1)直线DE与⊙O相切.
理由如下:连接OD.
∵AD平分∠BAC,
∴∠EAD=∠OAD.
∵OA=OD,
∴∠ODA=∠OAD.
∴∠ODA=EAD.
∴EA∥OD.
∵DE⊥EA,
∴DE⊥OD.
又∵点D在⊙O上,∴直线DE与⊙O相切.
(2)如图,作DF⊥AB,垂足为F.

∴∠DFA=∠DEA=90°.
∵∠EAD=∠FAD,AD=AD,
∴△EAD≌△FAD.
∴AF=AE=8,DF=DE.
∵OA=OD=5,∴OF=3.
在Rt△DOF中,由勾股定理,得DF=4
∴DE=DF=4.
考点:切线的性质和判定,勾股定理


科目:初中数学 来源:2013-2014学年新疆阿拉尔市九年级秋季班第一次月考数学试卷(解析版) 题型:选择题
把抛物线 向右平移3个单位,再向下平移2个单位,所得图象的解析式是
向右平移3个单位,再向下平移2个单位,所得图象的解析式是 ,则有( )
,则有( )
A. ,
, B.
B. ,
,
C. ,
, D.
D.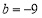 ,
,
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市海怡翠学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
等腰三角形的一边为4,另一边为9,则这个三角形的周长为( )
A.17 B.22 C.13 D.17或22
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省英文实验学校九年级上学期第一次月考数学试卷(解析版) 题型:填空题
把 化为一般形式后是_________________________其中方程中的a=______,b=__________,c=________。
化为一般形式后是_________________________其中方程中的a=______,b=__________,c=________。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省英文实验学校九年级上学期第一次月考数学试卷(解析版) 题型:选择题
顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )
①平行四边形;②菱形;③等腰梯形;④对角线互相垂直的四边形。
A.① ③ B.② ③ C.③④ D.②④
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省淄博市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB
是⊙O的直径,D是BC的中点.

(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,ΔABC还需满足什么条件,点E才一定是AC的中点?(直接写出
结论).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省淄博市九年级上学期期中考试数学试卷(解析版) 题型:选择题
若二次函数 的
的 与
与 的部分对应值如下表,则当
的部分对应值如下表,则当 =1时,
=1时, 的值为( )
的值为( )
| -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | ﹣3 | 3 | 5 | 3 |
A.5 B.﹣3 C.-13 D.-27
查看答案和解析>>
科目:初中数学 来源:2013-2014学年天津市和平区结课考试数学试卷(解析版) 题型:解答题
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点,当它靠在另一侧墙时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离DE=  m,求点B到地面的垂直距离BC.
m,求点B到地面的垂直距离BC.

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省金华市金东区九年级4月中考模拟数学试卷(解析版) 题型:选择题
下列各式,能用平方差公式计算的是( )
A.(x+2y)(2x-y) B.(x+y)(x-2y)
C.(x+2y)(2y-x) D.(x-2y)(2y-x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com