
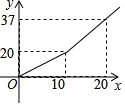
 为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,超出的部分按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:按上述分段收费标准,小兰家3月份和4月份分别交水费29.1元和20.8元,则小兰家4月份比3月份节约用水4.9吨.
为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,超出的部分按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:按上述分段收费标准,小兰家3月份和4月份分别交水费29.1元和20.8元,则小兰家4月份比3月份节约用水4.9吨. 分析 设y与x之间的函数关系式为y=kx+b,把点(10,20),(20,37)代入得到方程组,即可得到函数解析式,把y=29.1和20.8代入函数解析式即可得到结论.
解答 解:(1)由函数图象可知,小兰家3月份和4月份分别交水费29.1元和20.8元,
∴x>10t,
当x>10时,设y与x之间的函数关系式为y=kx+b,
把点(10,20),(20,37)代入得:$\left\{\begin{array}{l}{10k+b=20}\\{20k+b=37}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1.7}\\{b=3}\end{array}\right.$,
∴y=1.7x+3,
当y=29.1时,即29.1=1.7x+3,
解得x=15.4,
当y=20.8时,即20.8=1.7x+3,
解得x=10.5,
∴小兰家4月份比3月份节约用水15.4-10.5=4.9,
故答案为:4.9.
点评 本题主要考查了一次函数与图形的结合,解决本题的关键是应注意分段函数的计算方法.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
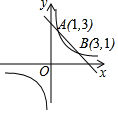 函数y1=$\frac{k}{x}$与y2=ax+b的图象在同一直角坐标系中如图所示,当y1<y2时,x的取值范围是( )
函数y1=$\frac{k}{x}$与y2=ax+b的图象在同一直角坐标系中如图所示,当y1<y2时,x的取值范围是( )| A. | 1<x<3 | B. | x<1 | C. | x<0或1<x<3 | D. | x<1或x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别是A(-3,2),B(-1,4),C(0,2)
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别是A(-3,2),B(-1,4),C(0,2)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB∥CD,AD∥BC | B. | AB=AD,CB=CD | C. | AB=CD,AC=BD | D. | ∠A=∠B,∠C=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com