
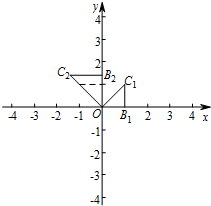
 已知:如图,在平面直角坐标系xOy中,点B1,C1的坐标分别为(1,0),(1,1).将△OB1C1绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2;将△OB2C2绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3.如此下去,得到△OBnCn.
已知:如图,在平面直角坐标系xOy中,点B1,C1的坐标分别为(1,0),(1,1).将△OB1C1绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2;将△OB2C2绕原点O逆时针旋转90°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3.如此下去,得到△OBnCn. 分析 (1)易得OB2=mOB1=OC1,根据最初的三角形中OB1,OC1的关系可得m的值;
(2)可得旋转4次后,正好旋转一周,那么可得点C2016的坐标跟C1的坐标在一条射线上,且在第四象限,即可得出结果.
解答 解:(1)在△OB1C1中,
∵OB1=1,B1C1=1,∠OB1 C1=90°,
∴∠C1OB1=45°,OC1=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∵OB2=mOB1,OB2=OC1,
∴m=$\sqrt{2}$.
故答案为:$\sqrt{2}$;
(2)∵每一次的旋转角是90°,
∴旋转4次后,正好旋转一周,
∴2016÷4=504,
∴点C2016跟C1的在一条射线上,且在第四象限,
∵第2次旋转后,各边长是原来的$\sqrt{2}$倍,第3次旋转后,各边长是原来的$\sqrt{2}$2倍,
∴点C2016的纵坐标为-$\sqrt{2}$2015.
故答案为:-${\sqrt{2}}^{2015}$.
点评 本题考查了坐标与图形的变化-旋转,等腰直角三角形的性质,勾股定理等知识,求出m的值和找出规律是解题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
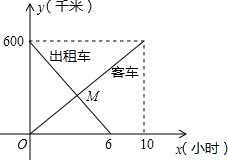 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示.
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
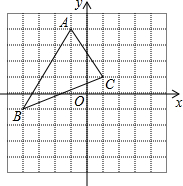 如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)
如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
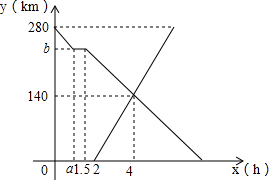 甲、乙两车分别从A、B两地沿着一条笔直的公路行驶,甲车从A地开往B地,2h后乙车从B地开往A地,两车均以各自的速度匀速行驶,甲车在行驶途中出观故障,停车维修0.5h后又以原速继续匀速行驶到B地,如图是甲、乙两车与B地的距离y(km)与甲车离开A地时间x(h)之间的函数图象,根据图象解答下列问题:
甲、乙两车分别从A、B两地沿着一条笔直的公路行驶,甲车从A地开往B地,2h后乙车从B地开往A地,两车均以各自的速度匀速行驶,甲车在行驶途中出观故障,停车维修0.5h后又以原速继续匀速行驶到B地,如图是甲、乙两车与B地的距离y(km)与甲车离开A地时间x(h)之间的函数图象,根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com