
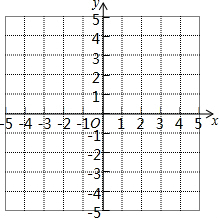
 ��֪����������y1=$\frac{k}{x}$�Ͷ��κ���y2=-x2+bx+c��ͼ����A��-1��2��
��֪����������y1=$\frac{k}{x}$�Ͷ��κ���y2=-x2+bx+c��ͼ����A��-1��2������ ��1������A����������������Ľ���ʽ�м��ɵó�k��ֵ���Լ�b��c��������ϵ��
��2���ڣ�1�����ѵó��˷����������Ľ���ʽ����ô�ɸ���B��C���㶼�ڷ����������Ͽ����B��C�����꣬Ȼ�����B��C�������ô���ϵ������������ߵĽ���ʽ�������ɸ����������Ľ���ʽ���ó�������ͼ�Σ��Լ�y1��y2ʱ��x��ȡֵ��Χ��
��3�����������߿������£���˶Գ�����ߣ��������ϵĵ㶼����x�������������ô�Գ���-$\frac{b}{2a}$��-$\frac{1}{2}$��Ȼ���ٸ��ݣ�1����b��c�Ĵ�С��ϵ�������c��ȡֵ��Χ��
��� �⣺��1����A��-1��2�����뷴��������y1=$\frac{k}{x}$�У�
�ɵ�k=��-1����2=-2��
��A��-1��2����������y2=-x2+bx+c��
�ɵ�2=-1-b+c��
��b=c-3��
��2���������֪��B������Ϊ��-2��1����C������Ϊ��1��-2����
�����������Ľ���ʽΪy1=-$\frac{2}{x}$��
�����ߵĽ���ʽΪy2=-x2-2x+1��
��ͼ��ͼ����ͼ��֪����x��-2��-1��x��0��1��xʱ��y1��y2��
��3���������߿������£���˶Գ�����ߣ��������ϵĵ㶼����x�����������
��-$\frac{b}{2a}$��-$\frac{1}{2}$��
��-$\frac{c-3}{-2}$��-$\frac{1}{2}$��
���c��2��
���� ������Ҫ�����˷����������Ͷ��κ������ۺ�֪ʶ������������ȷ��b��c��ֵ��������ϵ�ǽ���Ĺؼ���


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{5}+\frac{y}{4}=\frac{42}{60}}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{4}+\frac{y}{5}=\frac{42}{60}}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{5}+\frac{y}{4}=42}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{4}+\frac{y}{5}=42}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
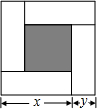 ��ͼ���������εı߳�Ϊm��С�����εı߳�Ϊn������x��y��ʾ�ĸ���ͬ�����ε����߳���x��y�����������¹�ϵʽ����x+y=m����x-y=n����xy=$\frac{{m}^{2}-{n}^{2}}{4}$�� ������ȷ�Ĺ�ϵʽ�ĸ����У�������
��ͼ���������εı߳�Ϊm��С�����εı߳�Ϊn������x��y��ʾ�ĸ���ͬ�����ε����߳���x��y�����������¹�ϵʽ����x+y=m����x-y=n����xy=$\frac{{m}^{2}-{n}^{2}}{4}$�� ������ȷ�Ĺ�ϵʽ�ĸ����У�������| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
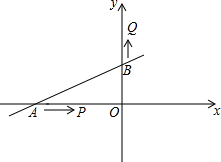 ֱ��y=$\frac{1}{2}$x+2��x����A����y����B��P���A�����������AO�˶���ͬʱQ��B�����������OB�����˶����ٶȾ�Ϊ1����λ/��
ֱ��y=$\frac{1}{2}$x+2��x����A����y����B��P���A�����������AO�˶���ͬʱQ��B�����������OB�����˶����ٶȾ�Ϊ1����λ/���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com