
数学活动﹣求重叠部分的面积
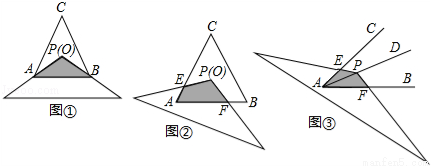
(1)问题情境:如图①,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点P与等边△ABC的内心O重合,已知OA=2,则图中重叠部分△PAB的面积为  .
.
(2)探究1:在(1)的条件下,将纸片绕P点旋转至如图②所示位置,纸片两边分别与AC,AB交于点E,F,图②中重叠部分的面积与图①重叠部分的面积是否相等?如果相等,请给予证明;如果不相等,请说明理由.
(3)探究2:如图③,若∠CAB=α(0°<α<90°),AD为∠CAB的角平分线,点P在射线AD上,且AP=2,以P为顶点的等腰三角形纸片(纸片足够大)与∠CAB的两边AC,AB分别交于点E、F,∠EPF=180°﹣α,求重叠部分的面积.(用α或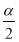 的三角函数值表示)
的三角函数值表示)
科目:初中数学 来源:2014-2015学年湖北省黄冈市中考模拟数学试卷(解析版) 题型:填空题
已知二次函数y=a(x+1)²-b (a≠0)的最小值是1,则a_____b.(>,≥,<或≤)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市燕山区中考一模数学试卷(解析版) 题型:解答题
阅读下面材料:小军遇到这样一个问题:如图1,△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围.

(1)小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:AD的取值范围是 .
(2)参考小军思考问题的方法,解决问题:如图3,△ABC中,E为AB中点,P是CA延长线上一点,连接PE并延长交BC于点D.求证:PA•CD=PC•BD.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市燕山区中考一模数学试卷(解析版) 题型:选择题
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于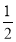 AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
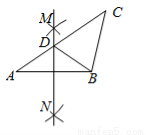
A.40° B.50° C.60° D.70°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市燕山区中考一模数学试卷(解析版) 题型:选择题
据报道,中国内地首次采用“全无人驾驶”的燕房线地铁有望年底完工,列车通车后将极大改善房山和燕山居民的出行条件,预计年输送乘客可达7300万人次,将7300用科学记数法表示应为( )
A.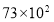 B.
B.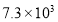 C.
C.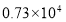 D.
D.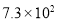
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:解答题
如图,一次函数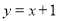 的图象与反比例函数
的图象与反比例函数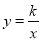 (
(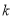 为常数,且
为常数,且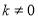 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).

(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数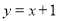 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县中考一模数学试卷(解析版) 题型:填空题
请写出一个开口向上,并且与y轴交于点(0,-2)的抛物线的表达式__________ .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
阅读下面的材料:
小敏在数学课外小组活动中遇到这样一个问题:
如果α,β都为锐角,且 ,
,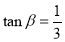 ,求
,求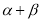 的度数.
的度数.
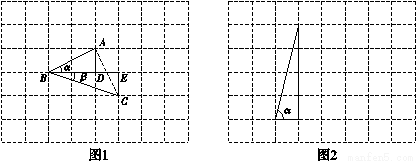
小敏是这样解决问题的:如图1,把 ,
,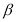 放在正方形网格中,使得
放在正方形网格中,使得 ,
,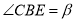 ,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得
,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得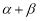 =∠ABC =
=∠ABC =
°.
请参考小敏思考问题的方法解决问题:
如果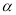 ,
, 都为锐角,当
都为锐角,当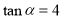 ,
, 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=
时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON= ,由此可得
,由此可得 =______°.
=______°.
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东莱芜卷)数学(解析版) 题型:选择题
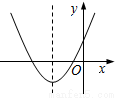
二次函数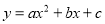 的图象如图所示,则一次函数
的图象如图所示,则一次函数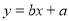 的图象不经过( )
的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com