
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
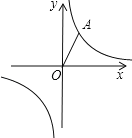
(1)试确定此反比例函数的解析式;
(2)将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
【答案】(1)y=![]() ;(2)点B(
;(2)点B(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
【解析】
试题分析:(1)作AC⊥x轴于点C,在Rt△AOC中,解直角三角形求得A点坐标为(1,![]() ),把A(1,
),把A(1,![]() )分别代入代入y=
)分别代入代入y=![]() ,根据待定系数法即可求得;
,根据待定系数法即可求得;
(2)作BD⊥x轴于点D,在Rt△BOD中,解直角三角形求得B点坐标为(![]() ,1),把x=
,1),把x=![]() 代入代入y=
代入代入y=![]() ,即可判断.
,即可判断.
解:(1)作AC⊥x轴于点C,如图,
在Rt△AOC中,
∵OA=2,∠AOC=60°,
∴∠OAC=30°,
∴OC=![]() OA=1,AC=
OA=1,AC=![]() OC=
OC=![]() ,
,
∴A点坐标为(1,![]() ),
),
把A(1,![]() )代入y=
)代入y=![]() ,
,
得k=1×![]() =
=![]() ,
,
∴反比例函数的解析式为y=![]() ;
;
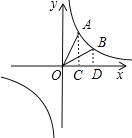
(2)点B在此反比例函数的图象上,
理由如下:过点B作x轴的垂线交x轴于点D,
∵线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,∴∠BOD=30°,
在Rt△BOD中,BD=![]() OB=1,OD=
OB=1,OD=![]() BD=
BD=![]() ,
,
∴B点坐标为(![]() ,1),
,1),
∵当x=![]() 时,y=
时,y=![]() =1,
=1,
∴点B(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=x2-(2m-1)x-6m与x轴交于(x1,0)和(x2,0)两点,已知x1x2=x1+x2+49,要使此抛物线经过原点,应将它向右平移__________个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 为
为![]() 中点,
中点, ![]() 、
、![]() 与射线
与射线![]() 分别相交于点
分别相交于点![]() 、
、![]() (射线
(射线![]() 不经过点
不经过点![]() ).
).
(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四形;
(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:AM=AN
(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:∠EMD=∠FND.
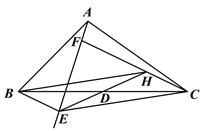
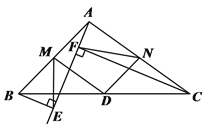
图① 图②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com