
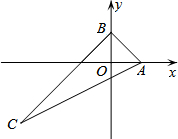
 如图,△ABC在平面直角坐标系中,点A、B分别在x轴和y轴上,且OA=OB,边AC所在直线解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,若△ABC的内心在y轴上,则tan∠ACB的值为( )
如图,△ABC在平面直角坐标系中,点A、B分别在x轴和y轴上,且OA=OB,边AC所在直线解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,若△ABC的内心在y轴上,则tan∠ACB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 △ABO是等腰直角三角形,然后根据△ABC的内心在y轴上,则BO是∠ABC的平分线,△ABC是直角三角形,求得BC的解析式,进而求得BC的长,然后根据三角函数的定义求解.
解答 解:在y=$\frac{1}{2}$x-$\frac{1}{2}$中,令y=0,则$\frac{1}{2}$x-$\frac{1}{2}$=0,解得x=1,
∵OA=OB,
∴B的坐标是(0,1),AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,△OAB是等腰直角三角形.
∵△ABC的内心在y轴上,
∴∠ABC=2∠ABO=90°,即△ABC是直角三角形,
设BC的解析式是y=x+c,
则把(0,1)代入得c=1,
则BC的解析式是y=x+1,
根据题意得:$\left\{\begin{array}{l}{y=\frac{1}{2}x-\frac{1}{2}}\\{y=x+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$,
即C的坐标是(-3,-2).
则BC=$\sqrt{{3}^{2}+(-2-1)^{2}}$=3$\sqrt{2}$,
则tanACB=$\frac{AB}{BC}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$.
故选B.
点评 本题考查了一次函数的性质以及三角形的内切圆,根据内心的性质说明△ABC是直角三角形是本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 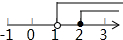 | B. | 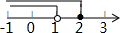 | C. | 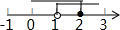 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 鞋厂检查生产鞋底能承受的弯折次数 | |
| C. | 学校招聘新教师,对应聘教师面试 | |
| D. | 某中学调查九年级全体540名学生的平均身高 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=$\frac{a}{x}$与正比例函数y=bx在同一坐标系中的大致图象可能是( )
二次函数y=ax2+bx+c的图象如图所示,反比例函数y=$\frac{a}{x}$与正比例函数y=bx在同一坐标系中的大致图象可能是( )| A. | 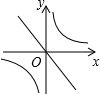 | B. | 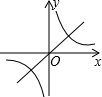 | C. | 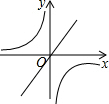 | D. | 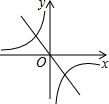 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com