
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
科目:初中数学 来源: 题型:解答题
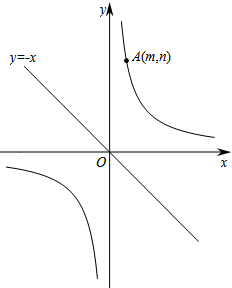 如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上.
如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,并拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.求旗杆AB的高度和小明后退的距离EC.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1m)
小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,并拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.求旗杆AB的高度和小明后退的距离EC.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在升旗结束后,小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小明从绳子末端C处拿起绳子放在头顶,后退至E点,此时绳子末端D与旗杆的顶端A成45°仰角,已知小明身高DE=1.6m,如图,求旗杆AB的高度和小明后退的距离.(单位:米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留一位小数)
在升旗结束后,小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小明从绳子末端C处拿起绳子放在头顶,后退至E点,此时绳子末端D与旗杆的顶端A成45°仰角,已知小明身高DE=1.6m,如图,求旗杆AB的高度和小明后退的距离.(单位:米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
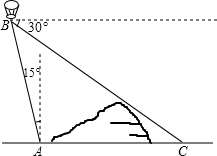 如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号)
如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com